Ultimo aggiornamento: 02/01/2022
Che cos' è una funzione?
Come si trova il dominio di una funzione?
Come si classificano le funzioni?
Ciao! Sono Giuseppe.
In questo blog pubblico
Ok, se mi segui, sarà tutto più semplice! 😃
In questo blog pubblico
esercizi svolti di matematica
per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo più di 5 esercizi svolti. Alla fine troverai un test di autovalutazione che ti invito a fare.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo più di 5 esercizi svolti. Alla fine troverai un test di autovalutazione che ti invito a fare.
Ok, se mi segui, sarà tutto più semplice! 😃
Adesso rispondiamo alla prima domanda, fornendo una
definizione di funzione:
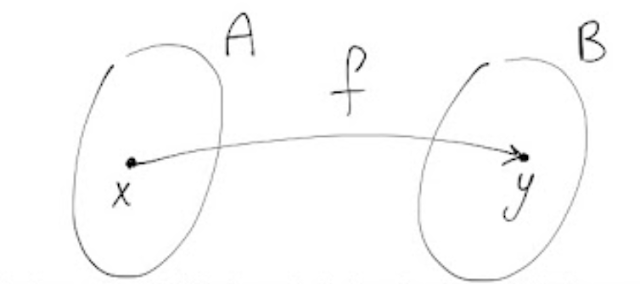
Una funzione f che va da un insieme A ad un insieme B è una relazione che associa ad ogni elemento x dell' insieme di partenza, A, uno ed un solo elemento y dell' insieme di arrivo, B.
 |
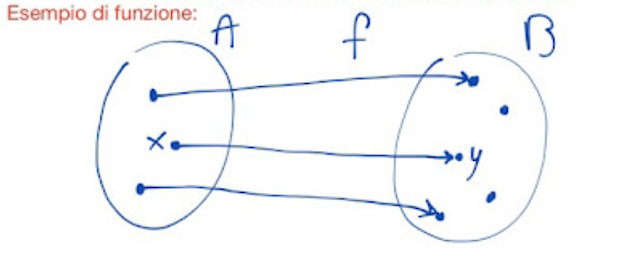| Fig. 1 |
 |
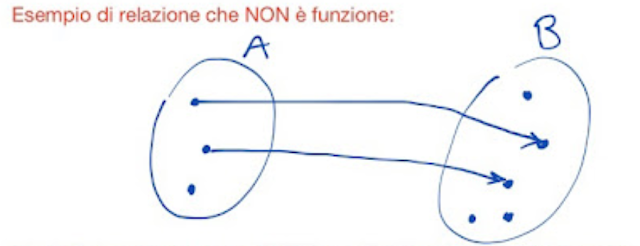| Fig. 2 |
La relazione rappresentata in fig. 2 non è una funzione perché non tutti gli elementi dell' insieme A hanno elementi associati (corrispondenti) nell'insieme B.
 |
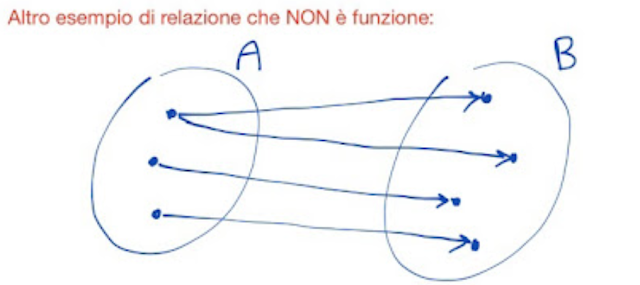| Fig. 3 |
La relazione rappresentata nella fig. 3, nonostante tutti gli elementi di A abbiano elementi associati (corrispondenti) in B, non è una funzione perché c'è un elemento di A al quale vengono associati due elementi di B.
Ricordiamo che si tratta di funzione quando ad ogni elemento di A (insieme di partenza) corrisponde uno ed un solo elemento di B (insieme di arrivo).
La scrittura f: A→B significa che la funzione f "pesca" elementi dell'insieme A e li "trasforma" in elementi dell'insieme B.
Una funzione può essere immaginata (fig. 4 qui sotto) come una scatola in cui entra un elemento x (input) ed esce uno ed un solo elemento y (output):
 |
| Fig. 4 |
La scrittura y=f(x) vuol dire proprio che la funzione f agisce sull'elemento x e lo trasforma in uno ed un solo elemento y.
Facciamo un esempio.
Prima di andare avanti, ci tengo a dirti che puoi imparare di più e finalmente puoi iniziare a migliorare i tuoi voti in matematica attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è
Matematica Quinquennio
Se vuoi imparare a risolvere gli esercizi di matematica con più serenità e abilità, allora è arrivato il momento di iniziare il tuo percorso gratuito; fai click sul link qui sotto:
Bene, torniamo all' esempio:
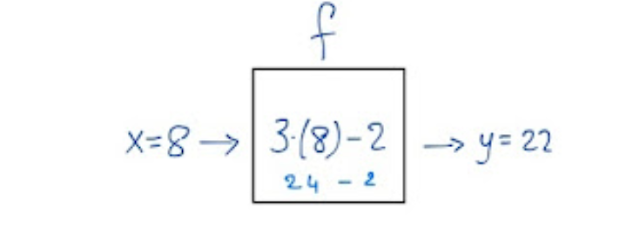
Sia y=3x-2 una relazione. Essa è una funzione.
Se facciamo entrare (fig. 5 qui sotto) l'elemento x=8 nella "scatola", uscirà un solo elemento, y=22.
 |
| Fig. 5 |
Adesso vediamo (fig. 6 qui sotto) che cosa si intende per elemento immagine.
 |
| Fig. 6 |
L'elemento y dell'insieme B si dice immagine dell'elemento x, secondo la funzione f .
Dominio e codominio di una funzione: che cosa sono?
 |
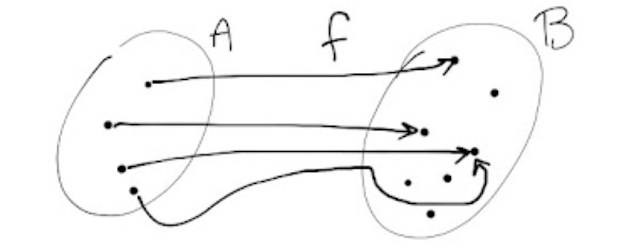| Fig. 7 |
L'insieme di partenza della funzione f è detto dominio; esso contiene tutti gli elementi su cui può operare, o agire, la funzione.
Esempio n. 1 sul dominio:
La funzione y=2x+1 ha come dominio tutto l'insieme dei numeri reali, R, perché può agire su tutti i numeri reali:
infatti ha senso moltiplicare per 2 un numero reale qualunque e poi aggiungergli 1 (y=2x+1).
In altre parole, come si vede nella fig. 8 qui sotto, possiamo mettere dentro la "scatola" della funzione f qualunque numero reale x:
 |
| Fig. 8 |
Esempio n.2 sul dominio:
La funzione y=2/x ha come dominio tutto l'insieme dei numeri reali, escluso x=0, perché questa particolare funzione può agire su tutti i numeri reali diversi da zero:
infatti non ha senso dividere 2 per zero; in generale, non si può dividere per zero!!
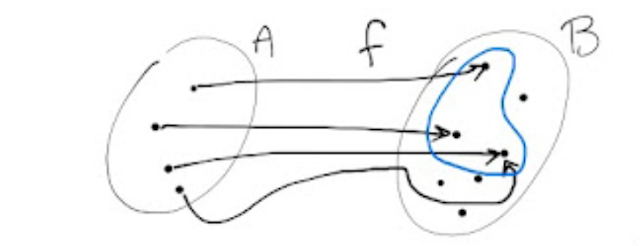
Il codominio di una funzione f , invece, è il sottoinsieme di B che contiene tutte le immagini degli elementi di A, secondo la funzione f.
Nella fig. 9 qui sotto, il codominio è costituito dagli elementi di B circondati dalla linea chiusa di colore blu:
 |
| Fig. 9 |
Dominio e codominio di una funzione: come individuarli in modo rapido e pratico, a partire dal grafico
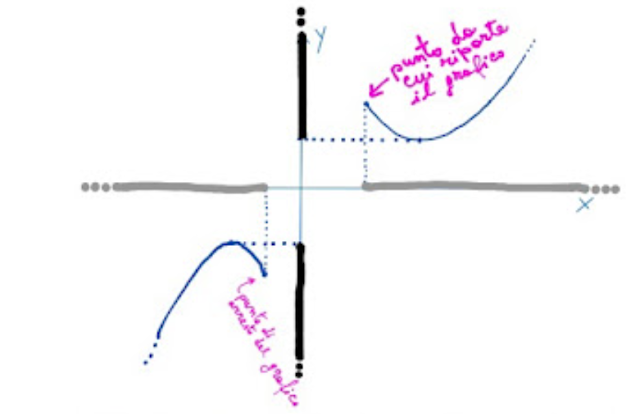
Se abbiamo il grafico di una funzione su un piano cartesiano (fig. 10 qui sotto), il dominio è dato dalla proiezione ("ombra grigia") della curva sull'asse x; mentre il codominio è dato dalla proiezione ("ombra nera") della curva sull'asse y.
 |
| Fig. 10 |
Il dominio della funzione, il cui grafico nella fig.10 è dato dalla curva di colore blu, è rappresentato dalle due semirette grigie giacenti sull'asse x, mentre il codominio della funzione è rappresentato dalle due semirette nere giacenti sull'asse y.
Funzione reale di variabile reale: che cos'è?
Una funzione reale di variabile reale è una relazione che "pesca" numeri reali appartenenti all'insieme di partenza A e li "trasforma" in numeri reali appartenenti all'insieme di arrivo B.
f: A→B
A e B sono sottoinsiemi di R (insieme dei numeri reali).
Esercizio sul dominio:
Trova il dominio, D, della funzione
y=1+√(x+1)
Svolgimento
Notiamo che l'argomento della radice quadrata, √ , è
x+1
Esso deve essere maggiore o uguale a zero.
Dunque imponiamo
x+1 ≥ 0
Risolvendo questa semplicissima disequazione, si ottiene
x ≥ -1
Poiché la funzione assegnata ha senso per
x ≥ -1 ,
il dominio è dato proprio da tutti i numeri reali maggiori o uguali a
-1
Si può scrivere:
D: x ≥ -1
oppure
D={x∊R | x ≥ -1}
oppure
D=[-1, +∞ [
Osservazione:
la funzione non ha senso, ad esempio, per
x = -2
Infatti, -2 non è maggiore o uguale a -1, e se proviamo a metterlo al posto della x, otteniamo:
y=1+√(x+1)
👇
y=1+√(-2+1)=
= 1+√(-1) = ❓
Se operiamo soltanto coi numeri reali, non ha senso calcolare la radice quadrata di un numero negativo:
-1, in questo caso!
Funzioni: come si classificano
 |
| Fig. 11 |
Sono razionali intere le funzioni polinomiali, come, ad esempio, le due funzioni che ho scritto qui sotto:
y=x-1;
y=-3x³+7x-1
Sono razionali fratte le funzioni date come rapporto di polinomi, come, ad esempio, le due funzioni che trovi qui sotto:
y=(x-1)/(x+1);
y=(x²-2)/(5x³+x-1)
Sono irrazionali le funzioni in cui la x compare sotto il segno di radice, come, ad esempio, la funzione che ho riportato qui sotto:
y=∛(x-2)
Sono trascendenti le funzioni non algebriche, come, ad esempio, le seguenti tre funzioni:
y=10ˣ ;
y= log (x) ;
y= sin (x)
Dominio di una funzione: esercizi svolti
Determina il dominio delle seguenti quattro funzioni:
1) y=2x²+3x-1 ;
2) y=(2x+1)/(x-3) ;
3) y=√(x²-3x) ;
4) y=∛[-x/(3-5x)]
Svolgimento
1)
y=2x²+3x-1 è una funzione razionale intera (polinomiale).
Essa ha senso per ogni valore reale della variabile x, pertanto il suo dominio è tutto l'insieme dei numeri reali, R.
D=R
2)
y=(2x+1)/(x-3) è una funzione razionale fratta (rapporto di due polinomi).
Questa funzione ha senso per tutti i valori reali di x, esclusi quei valori che azzerano il denominatore.
Poniamo dunque il denominatore, x-3, uguale a zero ed escludiamo le soluzioni dell'equazione che deriva appunto dall'aver posto il denominatore uguale a zero.
L'equazione che otteniamo è
x-3=0
Siccome x=3 annulla il denominatore della funzione, essa per tale valore non ha senso.
Perché non ha senso?
Perché non ha senso dividere per zero!
Infatti, per x=3 si ha
y=(2⋅3+1)/(3-3)=
7/0 = impossibile!
Il suo dominio è dunque
D= R-{3} ,
oppure, più semplicemente, possiamo scrivere:
D: x≠3
3)
y=√(x²-3x)
Questa terza funzione ha senso per
x²-3x ≥ 0 ,
visto che l'espressione x²-3x si trova sotto la radice quadrata.
Più in generale, se lavoriamo soltanto coi numeri reali,
 |
| Fig. 12 |
Ecco, in base a quello che ho scritto nella fig. 12,
√(x²-3x) ha senso per x²-3x ≥ 0, perché l'indice di radice è n=2 (pari).
Dunque risolviamo la disequazione
x²-3x ≥ 0
Raccolgo il fattor comune, x, e riscrivo la disequazione così :
x(x-3) ≥ 0 .
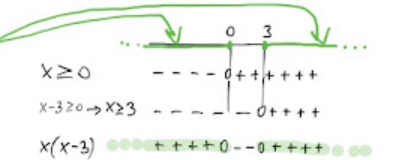
Studiamo il segno dei singoli fattori, x ed x-3, visualizzando le informazioni relative ai segni su un grafico:
 |
| Fig. 13 |
Poiché la funzione ha senso per
x(x-3) ≥ 0 ,
dobbiamo prendere i valori della x che appunto rendono il prodotto
x(x-3)
positivo o nullo ( ≥ 0)
 |
| Fig. 14 |
Come puoi vedere nella fig. 14, nell' intervallo ]-∞, 0[ , sia il fattore x che il fattore x-3 sono entrambi negativi, dunque il loro prodotto è positivo.
Nell' intervallo ]0, 3[ , il fattore x è positivo e il fattore
x-3 è negativo, dunque il loro prodotto è negativo.
Nell' intervallo ]3, +∞[ , sia il fattore x che il fattore x-3 sono entrambi positivi, dunque il loro prodotto è positivo.
Andiamo a vedere cosa succede in x=0 e in x=3.
In x=0 il fattore x vale, banalmente, zero, e dunque il prodotto tra i due fattori vale zero; in x=3 il fattore
x-3
vale zero, e dunque il prodotto tra i due fattori, anche qui, vale zero.
Ora, siccome la funzione ha senso per
x(x-3) ≥ 0 ,
domandiamoci in quali intervalli il prodotto
x⋅(x-3)
è positivo o nullo.
La figura 14 ci mostra che il dominio è dato dall' unione di due intervalli:
x≤0 oppure x≥3
Possiamo anche scrivere così:
D= ]-∞, 0] ⋃ [3, +∞[
4)
y=∛[-x/(3-5x)]
In questo caso, la radice è cubica; l' indice di radice è
n=3 (dispari).
Secondo lo schemino di fig. 12, la funzione ha senso sia per valori positivi o nulli di
-x/(3-5x)
sia per valori negativi.
L' unica cosa che non si deve verificare è l' annullamento del denominatore.
Deve essere
3-5x ≠ 0
Dobbiamo dunque risolvere l' equazione
3-5x=0
ed escludere poi la sua soluzione, che è
x=3/5
Questo è l' unico valore reale per cui non ha senso la funzione; esso azzera il denominatore dell' argomento della radice cubica.
Il suo dominio è quindi
D: x ≠ 3/5
Bene, adesso ti invito a fare il test di autovalutazione che trovi qui sotto:
Puoi seguire questa esercitazione anche nel video qui sotto:
Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)