In questa esercitazione, risolviamo quattro disequazioni, tra cui due sono fritte (ooops, scusate, volevo dire "fratte").
Ecco le prime due:
Ex. 1 (di 4)
Portiamo il -5 dal 2º al 1º membro, cambiandogli il segno. A destra del minore ( < ) rimane lo zero:
Qui il
minimo comune multiplo è 1-2x :
Dopo avere eseguito le varie operazioni, siamo giunti ad una disequazione del tipo
N/D < 0
N sta per Numeratore;
D sta per Denominatore.
Mettiamo ben in evidenza sia il Numeratore sia il Denominatore:
Studiamo il segno di
N e
D:
Ci chiediamo per quali valori della x il Numeratore(N) e il Denominatore(D) sono positivi:
Risolvendo le due semplici disequazioncine, abbiamo trovato che N è positivo per
x > -11/2, mentre D è positivo per x < 1/2.
Visualizziamo queste informazioni sui segni, disegnando appunto le linee dei segni:
In corrispondenza di x = -11/2, N si azzera ed è negativo per x < -11/2.
In corrispondenza di x = 1/2, D si azzera ed è negativo per x > 1/2.
Individuiamo 3 intervalli:
uno che va da -infinito a -11/2, uno compreso tra -11/2 e 1/2, l' altro che va da 1/2 a +infinito.
A noi interessa il segno del rapporto N/D. Vediamo:
Come si può vedere dalla linea dei segni relativa al rapporto
N/D, si ha che tale rapporto è positivo solamente nell' intervallo compreso tra -11/2 e 1/2, ed è negativo altrove.
Notiamo, in particolare, che N/D vale zero per x = -11/2, e in x = 1/2 non esiste (perchè non si può dividere per zero, giusto?).
Se non ti è chiaro qualcosa, fammelo sapere nei commenti.
Poichè la disequazione assegnata ci chiede per quali valori di x il rapporto
N/D è negativo ( < 0 ),
le soluzioni della disequazione sono quelle evidenziate in verde nella figura qui sotto:
N/D è negativo per x < -11/2 oppure (
v) per x > 1/2 .
Ecco qui sotto tre modi di scrivere le soluzioni della disequazione assegnata:
Ti ricordo che puoi chiedere nei commenti ciò che eventualmente non ti è chiaro.
Prima di iniziare ad affrontare il 2° esercizio, per non perderti i miei nuovi esercizi svolti, ti
invito a
Ex. 2 (di 4)
Portiamo al 1º membro il termine che si trova al 2º membro, cambiandone il segno:
Il minimo comune multiplo è il polinomio x+4 :
Dopo aver fatto le operazioni dovute, abbiamo ottenuto un
rapporto tra due polinomi.
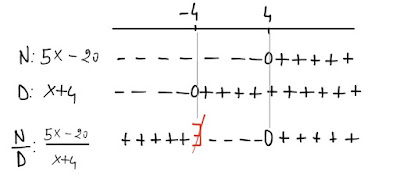
Abbiamo quindi un polinomio Numeratore ( 5x-20 ) e un polinomio Denominatore ( x+4 ), di cui studieremo i segni:
Ci chiediamo per quali valori della x il Numeratore e il Denominatore sono positivi, risolvendo due semplici, anche in questo caso, disequazioni:
Il Numeratore è positivo per x > 4, vale zero in x=4, ed è negativo per x < 4 .
Il Denominatore è positivo per x > -4, vale zero in x = -4, ed è negativo per x < -4 .
Queste informazioni vengono visualizzate con le linee dei segni che vedete qui sotto:
Individuiamo 3 intervalli:
Qui sotto potete vedere la linea dei segni relativa al rapporto
N/D :
Come si può osservare dalla figura, il rapporto N/D è positivo per tutte le x < -4, in quanto N e D hanno lo stesso segno (sono entrambi negativi);
il rapporto N/D è positivo anche per tutte le x > 4, in quanto N e D hanno lo stesso segno (sono entrambi positivi);
il rapporto N/D è negativo per tutti i valori compresi tra -4 e 4, -4 < x < 4, in quanto N e D hanno segni diversi (N è negativo e D è positivo);
Ora, facciamo attenzione a cosa succede nei capisaldi, -4 e 4:
in -4, N/D non ha senso (ecco il motivo di quella strana E rossa e tagliata, coi denti verso sinistra, che si legge "non esiste"), in quanto il Denominatore ( D ), per x = -4, vale zero (e voi sapete che non si può dividere per zero, vero?);
in 4, N/D è nullo, in quanto il Numeratore ( N ), per x = 4, si annulla, e il Denominatore è positivo (infatti zero diviso per un numero positivo fa zero).
Poichè la disequazione assegnata del nostro 2º esercizio è equivalente alla disequazione
(5x-20)/(x+4) > 0, le soluzioni sono date da quei valori della x che rendono tale rapporto ( N/D ) positivo.
La linea dei segni relativa al rapporto N/D ci dice che le soluzioni sono date dai numeri strettamente minori di -4 oppure da quelli strettamente maggiori di 4.
Ecco tre modi di rappresentare queste soluzioni:
Se hai domande, dubbi, osservazioni, fammi sapere nella sezione dedicata ai commenti.
Ecco gli ultimi due esercizi:
Ex. 3 (di 4)
Facciamo le operazioni:
Sommiamo i termini simili che troviamo nel 2º membro:
Continuando a "giocare" con l' algebra, facciamo in modo che tutti i termini, tranne
9x, siano al 1º membro ( attenzione ai segni ! ).
Poi semplifichiamo.
Abbiamo ottenuto che 4 è maggiore o uguale di 9x, oppure, leggendo da destra verso sinistra, si ha che 9x è minore o uguale a 4.
Dividiamo entrambi i membri per 9 (che è positivo) e si conclude dicendo che le soluzioni sono date da tutti i valori reali minori o uguali a 4/9
Ti faccio notare che una disequazione, normalmente, si legge da sinistra a destra, ma, giocando un pò, si può leggere da destra a sinistra.
Esempio: x-1 < 4+3x significa che x-1 è minore di 4+3x, ma vuol dire anche, leggendo da destra verso sinistra, che 4+3x è maggiore di x-1.
La semiretta qui sotto, con l' estremo destro incluso (pallino pieno) visualizza le soluzioni trovate.
La notazione che vedete sotto la semiretta indica l' intervallo, costituito dalle soluzioni trovate, che va da -infinito (sempre escluso) a 4/9 (incluso).
Ex. 4 (di 4)
Premetto che questa disequazione verrà risolta senza utilizzare gli "strumenti" delle disequazioni di 2º grado.
Quindi anche coloro che non hanno ancora affrontato le equazioni e disequazioni di 2º grado possono seguirmi nel ragionamento.
Pronti ?
Via !!
Vediamo due fattori, A e B, che si moltiplicano tra di loro:
Studiamo il segno di ciascun fattore:
Studiare il segno di un fattore significa porlo maggiore di zero ( > 0 ) e studiare la disequazione che ne deriva:
Vediamo le linee dei segni relative ai due fattori:
Il primo fattore, x-1, è positivo per valori di x maggiori di 1, vale zero in x=1, ed è negativo altrove;
Il secondo fattore, x+2, è positivo per valori di x maggiori di -2, vale zero in x = -2, ed è negativo altrove.
Qui sotto vediamo la linea dei segni dedicata al
prodotto tra i due fattori:
Negli intervalli in cui A e B sono concordi (cioè hanno lo stesso segno), il loro prodotto,
(x-1)(x+2), è positivo.
A•B è negativo laddove i due fattori sono discordi (cioè NON hanno lo stesso segno).
A•B è nullo nei punti in cui uno dei due fattori vale zero.
La disequazione assegnata vuole sapere per quali valori di x il prodotto tra i due fattori è minore o uguale a zero.
Nella figura qui sopra ho evidenziato in verde l' intervallo in cui il prodotto ė negativo o nullo.
Finiamo questa esercitazione scrivendo in uno dei modi possibili le soluzioni:
Le soluzioni sono tutti i valori reali compresi tra -2 e 1, estremi inclusi.
Bene, per non perderti i miei nuovi esercizi svolti, ti invito a