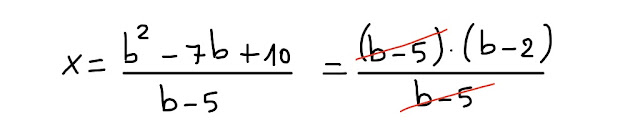Un altro motivo per cui le lezioni private, che possono essere personalizzate e tagliate su misura dello studente che le riceve, sono importanti e' il seguente:
come docente in classi scolastiche regolari, mi e' capitato di notare quanto siano presenti elementi di disturbo durante il normale svolgimento della lezione, nonostante gli interventi di natura disciplinare per richiamare la classe all' ordine e all' attenzione.
Tenendo conto della scarsa collaborazione di alcuni studenti che non favoriscono un clima, all' interno della classe, favorevole allo svolgimento della lezione e considerando le diverse velocità di apprendimento di ciascun allievo, il docente deve necessariamente puntare sulla velocità media dell' intera classe che vedrà più avvantaggiati gli studenti che hanno una velocità di apprendimento vicina a quella media. Passatemi questa metafora, che schematizza il concetto sulla difficoltà che uno studente puo' incontrare in classe nell' apprendere, in modo adeguato, una materia scolastica.
Faccio un esempio.
In una classe ci sono tre soli studenti, Gertrude, Aroldo ed Eustachio; la prima ha, da 1 a 10, una velocità di apprendimento pari a 5; il secondo viaggia sul 4,5; il terzo ha una velocità pari a 7,5.
La media della velocità di apprendimento della classe e' (5+4,5+7,5)/3=5,67. La studentessa che trarrà maggiori benefici da quelle lezioni e' Gertrude; le lezioni saranno meno adatte ad Aroldo e, paradossalmente, ancora meno adatte ad Eustachio, che avrebbe bisogno di uno standard un po' più alto. Eustachio si trova in una classe in cui non vengono sfruttate al meglio le sue potenzialità, mentre Aroldo si trova nella stessa classe in cui si tiene poco conto delle sue lacune e carenze.
Le lezioni private, invece, poiché sono personalizzate, sia sugli studenti bravi sia su quelli meno bravi, elimina il problema della velocità media, perché lo studente avrà un intervento didattico di supporto che intercetta pienamente la sua specifica velocità di apprendimento. Se si tratta di studente con delle insufficienze, il docente privato può intervenire sulle lacune; se si tratta di studente bravo, il tutor privato può intervenire potenziando le sue capacita' e abilita'.
Poiché la matematica e' ormai entrata quasi dappertutto, consiglio vivamente di intraprendere un percorso di apprendimento integrativo, parallelo e supplementare rispetto al corso regolare di matematica seguito a scuola.
CONTATTATEMI SENZA INDUGIO!
giusemath@gmail.com
Cerca nel blog
lunedì 30 settembre 2013
domenica 29 settembre 2013
TRASFORMAZIONE DEL GRAFICO DI UNA FUNZIONE
E' interessante sapere come cambia il grafico di f(x) se alla f(x) applico la radice quadrata.
Tutte le considerazioni possono essere visualizzate facendo clic QUI
Tutte le considerazioni possono essere visualizzate facendo clic QUI
venerdì 27 settembre 2013
CURIOSITÀ: simmetria e parole palindrome
Sfida.
La mia data di nascita, 27-11-72, e' PALINDROMA: possiede un asse di simmetria che possiamo immaginare tra 1 e 1 di UNDICI. Per tale motivo essa può essere letta sia da sinistra verso destra sia da destra verso sinistra.
Le parole o le frasi palindrome hanno questa proprieta': si leggono nei due versi; hanno, per così dire, un asse di simmetria. La simmetria e' un concetto importante in matematica ed anche in fisica!
Vi lancio una sfida:
riuscite a trovare parole o frasi palindrome, oltre a quelle che vi propongo io?
Comincio con quelle più facili:
ANNA
OTTO
INGEGNI
...
...
Più difficili:
AI LATI D' ITALIA
...
...
La mia data di nascita, 27-11-72, e' PALINDROMA: possiede un asse di simmetria che possiamo immaginare tra 1 e 1 di UNDICI. Per tale motivo essa può essere letta sia da sinistra verso destra sia da destra verso sinistra.
Le parole o le frasi palindrome hanno questa proprieta': si leggono nei due versi; hanno, per così dire, un asse di simmetria. La simmetria e' un concetto importante in matematica ed anche in fisica!
Vi lancio una sfida:
riuscite a trovare parole o frasi palindrome, oltre a quelle che vi propongo io?
Comincio con quelle più facili:
ANNA
OTTO
INGEGNI
...
...
Più difficili:
AI LATI D' ITALIA
...
...
giovedì 26 settembre 2013
TRASFORMAZIONI GEOMETRICHE: DAL GRAFICO ALLA FUNZIONE
Segui @ilmatematto
Vi propongo un esercizio interessante, per le idee che emergono, su come dedurre l' equazione di una funzione di cui si conosce soltanto il grafico e qualche altra informazione relativa ad esso. Per visualizzare lo svolgimento, fai clic QUI
Tags, etichette:
dal grafico all' equazione,
dal grafico alla funzione,
esercizi svolti sulle trasformazioni geometriche,
trasformazioni geometriche
mercoledì 25 settembre 2013
calcolo del periodo di una funzione
Segui @ilmatematto
Vi propongo un metodo potente, quando il gioco si fa duro, per calcolare in modo sicuro il periodo di una funzione. Per visualizzare, fai clic qui
Tags, etichette:
esercizi svolti sul periodo delle funzioni,
funzioni periodiche,
periodo di una funzione,
trovare il periodo di una funzione
FUNZIONE INVERSA
Prima di scaricare o visualizzare il materiale didattico che ti interessa, ISCRIVITI AL MIO CANALE YOUTUBE E CONDIVIDI. GRAZIE!!
IMPORTANTE : sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Voglio mostrarvi perché i grafici di due funzioni, l' una inversa dell' altra, sono simmetrici rispetto alla bisettrice del I e III quadrante. Per visualizzare i passaggi fate clic qui
IMPORTANTE : sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Voglio mostrarvi perché i grafici di due funzioni, l' una inversa dell' altra, sono simmetrici rispetto alla bisettrice del I e III quadrante. Per visualizzare i passaggi fate clic qui
Tags, etichette:
come si disegna la funzione inversa,
funzione inversa,
funzioni inverse,
simmetria rispetto alla bisettrice del primo e terzo quadrante
come in uno stereogramma...
A volte, quando si affronta un argomento di matematica, ma questo vale anche nelle altre materie di studio, si incontrano delle difficoltà: le cose che si leggono appaiono confuse e non si comprendono.
Può succedere, ma non bisogna arrendersi! Occorre insistere ed e' necessario porsi delle domande, cercare di visualizzare i concetti, metterli in relazione tra loro, fare degli schemi, fare degli esercizi e tornare sulla teoria. Una metafora e' data dallo stereogramma(immagine all' apparenza priva di senso, confusa), che, se osservato nella giusta maniera, mostra ciò che c' e' in profondità. Se guardi lo stereogramma nel modo corretto, senza mollare, senza arrenderti, riuscirai a vedere quello che sta sotto la superficie. Ciò che prima appariva caotico, poi appare con chiarezza e la soddisfazione e' innegabile. Ecco, un argomento difficile di matematica e' come uno stereogramma: in un primo momento ci fornisce un' immagine caotica, incomprensibile, ma poi, andando in profondità(come quando si fa un approfondimento dell' argomento), cogliamo l' immagine tridimensionale(come quando impariamo un nuovo concetto matematico). Un esempio di stereogramma può essere visualizzato facendo clic qui
Può succedere, ma non bisogna arrendersi! Occorre insistere ed e' necessario porsi delle domande, cercare di visualizzare i concetti, metterli in relazione tra loro, fare degli schemi, fare degli esercizi e tornare sulla teoria. Una metafora e' data dallo stereogramma(immagine all' apparenza priva di senso, confusa), che, se osservato nella giusta maniera, mostra ciò che c' e' in profondità. Se guardi lo stereogramma nel modo corretto, senza mollare, senza arrenderti, riuscirai a vedere quello che sta sotto la superficie. Ciò che prima appariva caotico, poi appare con chiarezza e la soddisfazione e' innegabile. Ecco, un argomento difficile di matematica e' come uno stereogramma: in un primo momento ci fornisce un' immagine caotica, incomprensibile, ma poi, andando in profondità(come quando si fa un approfondimento dell' argomento), cogliamo l' immagine tridimensionale(come quando impariamo un nuovo concetto matematico). Un esempio di stereogramma può essere visualizzato facendo clic qui
martedì 24 settembre 2013
Funzioni periodiche
Per chiarire ancora di più il concetto di funzione periodica, leggi queste note che ho preparato.
lunedì 23 settembre 2013
Curiosità matematiche: M' ama o non m' ama?
Quante volte vi e' capitato di chiedere ai petali di una margherita se la persona che vi fa battere il cuore vi ama oppure no?
La domanda che vi pongo, pero', e' un' altra: sapete quale relazione c' e' tra i petali di una margherita e i conigli?
Un famoso matematico pisano, Fibonacci, studio', dal punto di vista quantitativo, la riproduzione dei conigli e da questa indagine scoprì una particolare successione di numeri, divenuta importantissima per la sua diffusa presenza in natura.
Si tratta di: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34...Avete capito come si costruisce questa successione di numeri?
Si parte da 0 e 1, per poi farne la somma. La regola e' che un numero della successione di Fibonacci e' dato dalla somma dei due precedenti.
Torniamo alla mia domanda: cosa hanno in comune i conigli con le margherite?
La risposta, incredibilmente, e' che il numero dei petali di una margherita e' sempre un numero che fa parte della successione del matematico pisano, che trovo' questi numeri studiando proprio i conigli.
Dai conigli "nascono", per così dire, questi numeri speciali, che ritroviamo nei petali delle margherite e non solo.
Come vedete, nella successione ci sono numeri pari e numeri dispari; quindi se cominciamo a staccare il primo petalo con un "M' AMA", avremo l' amara risposta se il numero dei petali e' pari.
Dobbiamo dunque sperare che il numero dei petali sia dispari, se cominciamo con un "M' AMA".
Chi può sapere in anticipo se la margherita che abbiamo raccolto ha un numero pari o dispari di
petali?
Il mistero e la poesia dell' amore sono dunque salvi ;-)
Se volete approfondire l' argomento sui numeri di Fibonacci, vi suggerisco un libro veramente interessante, acquistabile subito facendo clic sull' icona riportata qui sotto:
La domanda che vi pongo, pero', e' un' altra: sapete quale relazione c' e' tra i petali di una margherita e i conigli?
Un famoso matematico pisano, Fibonacci, studio', dal punto di vista quantitativo, la riproduzione dei conigli e da questa indagine scoprì una particolare successione di numeri, divenuta importantissima per la sua diffusa presenza in natura.
Si tratta di: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34...Avete capito come si costruisce questa successione di numeri?
Si parte da 0 e 1, per poi farne la somma. La regola e' che un numero della successione di Fibonacci e' dato dalla somma dei due precedenti.
Torniamo alla mia domanda: cosa hanno in comune i conigli con le margherite?
La risposta, incredibilmente, e' che il numero dei petali di una margherita e' sempre un numero che fa parte della successione del matematico pisano, che trovo' questi numeri studiando proprio i conigli.
Dai conigli "nascono", per così dire, questi numeri speciali, che ritroviamo nei petali delle margherite e non solo.
Come vedete, nella successione ci sono numeri pari e numeri dispari; quindi se cominciamo a staccare il primo petalo con un "M' AMA", avremo l' amara risposta se il numero dei petali e' pari.
Dobbiamo dunque sperare che il numero dei petali sia dispari, se cominciamo con un "M' AMA".
Chi può sapere in anticipo se la margherita che abbiamo raccolto ha un numero pari o dispari di
petali?
Il mistero e la poesia dell' amore sono dunque salvi ;-)
Se volete approfondire l' argomento sui numeri di Fibonacci, vi suggerisco un libro veramente interessante, acquistabile subito facendo clic sull' icona riportata qui sotto:
domenica 22 settembre 2013
Introduzione informale al concetto di limite
Quello che vi propongo non e' un vero e proprio esercizio sui limiti, ma quasi un giochetto per introdurre in modo leggero uno dei concetti più importanti dell' Analisi Matematica: il limite di una funzione. Potete visualizzare il contenuto facendo clic qui.
Tags, etichette:
concetto di limite,
idea di limite di una funzione,
introduzione al concetto di limite,
significato di limite di una funzione
giovedì 19 settembre 2013
Esercizio sul metodo grafico per risolvere una disequazione
CIRCONFERENZA.
Un esercizio che a me piace molto, sul passaggio dal grafico alla disequazione, si può scaricare da qui
Un esercizio che a me piace molto, sul passaggio dal grafico alla disequazione, si può scaricare da qui
Esercizio di base sul fascio di circonferenze
Questo esercizio chiede il luogo geometrico descritto dai centri delle circonferenze del fascio. Potete scaricarlo da qui
Esercizio di base sull' asse radicale
L' esercizio chiede di trovare l' equazione dell' asse radicale di un fascio di circonferenze, di cui si conoscono le due generatrici. Potete scaricarlo da qui
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Esercizio di base sulla tangente ad una circonferenza
Un esercizio sulla tangente ad una circonferenza può essere scaricato da qui
Ancora sulla simmetria assiale
L' esercizio che vi propongo affronta la simmetria assiale in modo diverso da quello adottato in un esercizio che ho precedentemente pubblicato. Potete trovare i dettagli qui
Tags, etichette:
esercizi sulla simmetria assiale,
esercizi svolti sulle trasformazioni geometriche,
simmetria assiale,
trasformazioni geometriche
martedì 17 settembre 2013
Esercizio su grafici e trasformazioni
Un esercizio che spiega, passo dopo passo, come trasformare un grafico di funzione applicando le opportune trasformazioni può essere scaricato da qui
lunedì 16 settembre 2013
Grafici e Trasformazioni Geometriche
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Uno schema pratico per operare con le trasformazioni geometriche applicate ai grafici delle funzioni può essere scaricato da qui
L' enigma dei numeri primi
Vi suggerisco un video molto ben fatto, curato da un eminente giovane matematico, sul mistero che avvolge ancora i numeri primi.
Guardatelo e provate anche voi a risolvere questo importante e affascinante problema matematico, ancora irrisolto.
Se siete amanti della lettura e volete approfondire questo affascinante argomento, acquistate adesso il libro, facendo clic sull' icona riportata qui sotto:
Fate clic qui per guardare il video.
Guardatelo e provate anche voi a risolvere questo importante e affascinante problema matematico, ancora irrisolto.
Se siete amanti della lettura e volete approfondire questo affascinante argomento, acquistate adesso il libro, facendo clic sull' icona riportata qui sotto:
Fate clic qui per guardare il video.
domenica 15 settembre 2013
Problema sulle trasformazioni geometriche
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Data una parabola di partenza ed una di arrivo(la trasformata della prima parabola), determinare le relazioni coinvolte nella trasformazione. Potete scaricare da qui i passaggi e le relative considerazioni. Nota: sono in gioco una ROTAZIONE DI 90 GRADI ATTORNO ALL' ORIGINE DEGLI ASSI IN SENSO ORARIO ed UNA TRASLAZIONE DI VETTORE (3;1).
Tags, etichette:
esercizi svolti trasformazioni geometriche,
parabole trasformazioni geometriche,
rotazioni,
trasformazioni geometriche,
traslazioni
Esercizio sulla omotetia
Se volete sapere come viene trasformata una parabola che "subisce" una omotetia, potete scoprirlo facendo clic qui
Esercizio dimostrativo sulla rotazione
Condivido con voi un altro interessante esercizio sulla rotazione di 90 gradi in senso orario attorno all' origine degli assi cartesiani. Potete scaricarlo da qui
venerdì 13 settembre 2013
Esercizio dimostrativo sulla simmetria assiale
Trovo questo esercizio, che ho preparato per voi, molto interessante e lo condivido con voi qui
Esercizio di base sulle disequazioni in due variabili
Un interessante esercizio sulla rappresentazione di una porzione di piano attraverso le disequazioni in due variabili può essere scaricato da qui
Esercizio di base sul fascio di rette
Un interessante esercizio che riguarda l' equazione di un fascio di rette che comprende anche la retta perpendicolare all' asse x può essere scaricato da qui
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Esercizio di base sul verso di rotazione delle rette di un fascio
Un esercizio carino può essere scaricato da qui
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Tags, etichette:
esercizi risolti geometria analitica,
esercizi svolti rotazione rette fascio,
fascio rette esercizi,
verso rotazione rette fascio
Esercizio di base sul fascio di rette
Lo svolgimento dell' esercizio può essere scaricato da qui.
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
giovedì 12 settembre 2013
Esercizio di base sul coefficiente angolare
Come calcolare il coefficiente angolare di una retta passante per due punti puoi scoprirlo qui
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Tags, etichette:
coefficiente angolare,
come calcolare coefficiente angolare,
esercizi svolti coefficiente angolare,
geometria analitica,
retta
Esercizio di base sulla retta passante per due punti
Come calcolare se tre punti sono allineati potete scoprirlo qui
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Esercizio di base sulle parti proporzionali di un segmento
Vi propongo un semplice esercizio sulle parti proporzionali di un segmento che potete scaricare da qui
martedì 10 settembre 2013
Esercizio di base sul baricentro di un triangolo
Ho preparato una video lezione breve sul baricentro di un triangolo
Esercizio di base sul punto medio di un segmento
Se vuoi vedere come si calcolano le coordinate del punto medio di un segmento, devi fare clic qui
Esercizio di base sulla distanza tra due punti
Scarica da qui un esercizio elementare sul calcolo della distanza tra due punti
Esercizio di base sulle coordinate di un punto su un piano
Un esercizio di base può essere scaricato e visualizzato se fai clic qui
Importanza delle lezioni private di matematica
Se dovessi sintetizzare in due sole parole l' importanza delle lezioni private di matematica, direi CONFRONTO e CONFORTO.
Si sa che la matematica è tra le materie scolastiche più complicate e meno gradite dagli studenti.
Come una disciplina sportiva, la matematica richiede "allenamento", quasi quotidiano, e stimoli ad affrontarla col giusto atteggiamento.
Ecco, il Tutor privato è come un Personal Trainer, un Coach, un allenatore personale, capace di motivare e stimolare lo studente, di equipaggiarlo con mezzi sufficienti a vincere le "gare" che via via il giovane è chiamato ad affrontare.
Due elementi, però, secondo me, emergono tra tutti: il CONFRONTO e il CONFORTO.
CONFRONTO, perché lo studente dialoga e si rapporta con una persona di esperienza, facendo domande su ciò che non gli è chiaro, esponendo i dubbi e condividendo col docente privato il suo impegno nello studio.
CONFORTO, perché il sostegno da parte del tutor è assicurato quando lo studente si sente guidato e sostenuto nel suo percorso di apprendimento della materia, soprattutto quando il Tutor riconosce le potenzialità dello studente, che altrimenti, nel contesto di una classe regolare, rimarrebbero, con buona probabilità, inespresse.
CONFRONTO e CONFORTO, dunque, due buoni motivi per ricorrere ad un docente privato di matematica.
Si sa che la matematica è tra le materie scolastiche più complicate e meno gradite dagli studenti.
Come una disciplina sportiva, la matematica richiede "allenamento", quasi quotidiano, e stimoli ad affrontarla col giusto atteggiamento.
Ecco, il Tutor privato è come un Personal Trainer, un Coach, un allenatore personale, capace di motivare e stimolare lo studente, di equipaggiarlo con mezzi sufficienti a vincere le "gare" che via via il giovane è chiamato ad affrontare.
Due elementi, però, secondo me, emergono tra tutti: il CONFRONTO e il CONFORTO.
CONFRONTO, perché lo studente dialoga e si rapporta con una persona di esperienza, facendo domande su ciò che non gli è chiaro, esponendo i dubbi e condividendo col docente privato il suo impegno nello studio.
CONFORTO, perché il sostegno da parte del tutor è assicurato quando lo studente si sente guidato e sostenuto nel suo percorso di apprendimento della materia, soprattutto quando il Tutor riconosce le potenzialità dello studente, che altrimenti, nel contesto di una classe regolare, rimarrebbero, con buona probabilità, inespresse.
CONFRONTO e CONFORTO, dunque, due buoni motivi per ricorrere ad un docente privato di matematica.
lunedì 9 settembre 2013
domenica 8 settembre 2013
CURIOSITÀ MATEMATICHE: La poesia nella solitudine dei numeri primi
"La solitudine dei numeri primi" e' il titolo, che a me piace molto, di un libro di Paolo Giordano.
di Paolo Giordano.
I numeri primi, si sa, sono ancora oggi un po' misteriosi. Essi sono "distanti" l' uno dall' altro, fatta eccezione per il 2 e il 3.
Se i numeri primi li rappresentiamo sulla linea dei numeri naturali, vediamo che, se va bene, sono separati da almeno un numero pari.
Ad esempio, il 5 e il 7 sono separati dal numero 6. Il 17 e il 19 sono separati dal numero 18. Fatta eccezione per il 2 e il 3 che sono praticamente a "contatto" tra loro, nel senso che non c' e' nessun numero naturale che li separa, ci sono numeri primi che per "incontrarsi e abbracciarsi" devono attraversare un solo numero pari( questi sono detti primi gemelli) e altri che sono separati da molti altri numeri che non sono primi.
Ad esempio, il 23 e il 29 sono separati da ben 5 numeri non primi. La metafora dei numeri primi e' molto azzeccata per parlare della irriducibile distanza tra persone, quasi condannate alla solitudine.
Solo pochi, pochissimi, sembrano camminare mano nella mano, a stretto contatto l'uno con l' altro, come appunto il 2 e il 3.
Puoi acquistare questo bellissimo libro adesso, facendo clic sull' icona qui sotto:
I numeri primi, si sa, sono ancora oggi un po' misteriosi. Essi sono "distanti" l' uno dall' altro, fatta eccezione per il 2 e il 3.
Se i numeri primi li rappresentiamo sulla linea dei numeri naturali, vediamo che, se va bene, sono separati da almeno un numero pari.
Ad esempio, il 5 e il 7 sono separati dal numero 6. Il 17 e il 19 sono separati dal numero 18. Fatta eccezione per il 2 e il 3 che sono praticamente a "contatto" tra loro, nel senso che non c' e' nessun numero naturale che li separa, ci sono numeri primi che per "incontrarsi e abbracciarsi" devono attraversare un solo numero pari( questi sono detti primi gemelli) e altri che sono separati da molti altri numeri che non sono primi.
Ad esempio, il 23 e il 29 sono separati da ben 5 numeri non primi. La metafora dei numeri primi e' molto azzeccata per parlare della irriducibile distanza tra persone, quasi condannate alla solitudine.
Solo pochi, pochissimi, sembrano camminare mano nella mano, a stretto contatto l'uno con l' altro, come appunto il 2 e il 3.
Puoi acquistare questo bellissimo libro adesso, facendo clic sull' icona qui sotto:
Problema di base sui sistemi lineari
Condivido con voi un simpatico problemino di base che si risolve impostando un opportuno sistema lineare. Fate clic qui
Sistemi Lineari: Letterali Interi e Letterali Fratti
Ultimo Aggiornamento: 27/08/2019
Esercizio 1
Semplifico e ottengo x:
Esercizio 2
Svolgimento Es. 2
Discutere questo sistema letterale significa studiare cosa succede al variare del parametro b.
Osservando il denominatore, b-x, della prima equazione, devo imporre che esso sia diverso da zero, dunque
b≠x .
Ora moltiplico primo e secondo membro della prima equazione del sistema per b-x, ottenendo un' equazione equivalente alla prima equazione del sistema assegnato:
Dalla seconda equazione del sistema assegnato si ha che
y = x+2.
Adesso metto l' espressione x+2 nella y dell' equazione di Fig. 2.2 (metodo di sostituzione):
Se b ≠ 5, allora x = b-2.
Siccome y = x + 2,
y = b - 2 + 2 = b
La soluzione è quindi data dalla coppia (b-2, b)
Se b ≠ 5, il sistema è determinato.
∀ b ∈ R ( b ≠ 5 ), notiamo che
x = b - 2 rispetta la condizione x ≠ b
Se invece b = 5, il sistema assegnato diventa:
Dopo la sostituzione, si ha
35 - 25 + 5x = 5(x+2)
10 + 5x = 5x + 10
0⋅x = 0
Questa equazione ha infinite soluzioni e dunque il sistema è indeterminato.
Esercizio 1
Risolvi e discuti questo sistema letterale intero, in cui x ed y sono le incognite e a è il parametro che viaria nell' insieme dei numeri reali (a ∈ R):
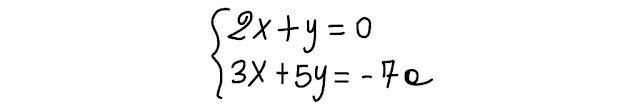 |
| Fig. 1.1 sistema letterale intero assegnato |
Svolgimento Es. 1
Scriviamo le due equazioni del sistema assegnato in forma esplicita:
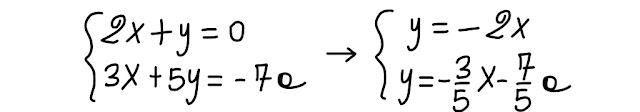 |
| Fig. 2.1 manipolazione algebrica |
Esse rappresentano le equazioni di due rette.
Possiamo notare che per ogni valore reale del
parametro a (∀ a ∈ R) le due rette sono incidenti, quindi il sistema possiede una sola soluzione (il sistema è determinato).
Andando avanti, si ha:
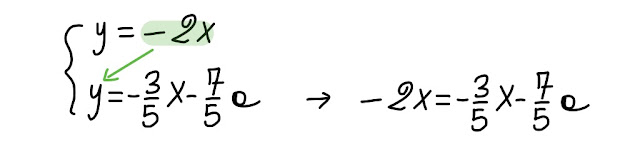 |
| Fig. 3.1 manipolazione algebrica: sostituzione |
Risolvo l' equazione di primo grado nell' incognita x ottenuta dopo la sostituzione:
 |
| Fig. 4.1 risoluzione dell' equazione di primo grado nell' incognita x |
 |
| Fig. 5.1 soluzione dell' equazione di primo grado nell' incognita x |
Di conseguenza, y = -2a
La soluzione del sistema è data dalla coppia (a, -2a)
Esercizio 2
Risolvi e discuti questo sistema letterale fratto, nelle incognite x ed y e parametro b ∊ R:
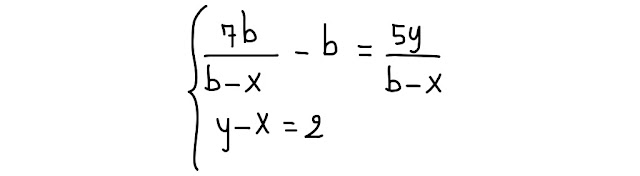 |
| Fig. 1.2 sistema letterale fratto assegnato |
Svolgimento Es. 2
Discutere questo sistema letterale significa studiare cosa succede al variare del parametro b.
Osservando il denominatore, b-x, della prima equazione, devo imporre che esso sia diverso da zero, dunque
b≠x .
Ora moltiplico primo e secondo membro della prima equazione del sistema per b-x, ottenendo un' equazione equivalente alla prima equazione del sistema assegnato:
 |
| Fig. 2.2 manipolazione della 1^ equazione del sistema |
Dalla seconda equazione del sistema assegnato si ha che
y = x+2.
Adesso metto l' espressione x+2 nella y dell' equazione di Fig. 2.2 (metodo di sostituzione):
 |
| Fig. 3.2 manipolazione algebrica: sostituzione |
Vado avanti e semplifico:
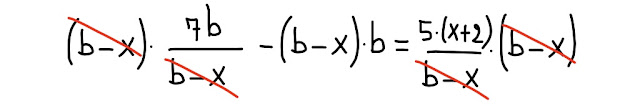 |
| Fig. 4.2 manipolazione algebrica: semplificazione |
Se b ≠ 5, allora x = b-2.
Siccome y = x + 2,
y = b - 2 + 2 = b
La soluzione è quindi data dalla coppia (b-2, b)
Se b ≠ 5, il sistema è determinato.
∀ b ∈ R ( b ≠ 5 ), notiamo che
x = b - 2 rispetta la condizione x ≠ b
Se invece b = 5, il sistema assegnato diventa:
 |
| Fig. 6.2 metodo di sostituzione |
Dopo la sostituzione, si ha
35 - 25 + 5x = 5(x+2)
10 + 5x = 5x + 10
0⋅x = 0
Questa equazione ha infinite soluzioni e dunque il sistema è indeterminato.
Tags, etichette:
sistemi letterali con discussione,
sistemi letterali fratti esercizi,
sistemi letterali interi esercizi,
sistemi lineari esercizi
Sistemi lineari numerici fratti
Ultimo aggiornamento: 20 agosto 2019
In questa esercitazione, prima di affrontare un sistema di equazioni fratte, voglio farti vedere come si calcola il determinante di una matrice quadrata 2 x 2.
Esercizio 1
Svolgimento Es. 1
Sui libri puoi trovare un altro modo di rappresentare il determinante di una matrice quadrata, come puoi vedere nella Fig. 2.1 qui sotto:
E' una notazione che ricorda il valore assoluto, ma in questo contesto specifico relativo alle matrici quadrate essa indica il determinante.
Ecco la regola:
Come puoi vedere nella Fig. 3.1, abbiamo due diagonali, una diagonale "a→d" e l' altra diagonale "c→b".
La regola dice:
facciamo il prodotto tra i due elementi della prima diagonale e poi togliamo il prodotto tra i due elementi della seconda diagonale.
Qui sotto, nella Fig. 4.1, puoi vedere l' applicazione di questa semplice regola per trovare il determinante richiesto dal nostro esercizio:
Esercizio 2
Svolgimento Es. 2
Come prima cosa, dobbiamo controllare le condizioni di esistenza (C. E.).
Dobbiamo imporre che
y ≠ 0, x ≠ 0, y ≠ 2
Perché imponiamo queste condizioni?
Perché i denominatori presenti nel sistema non possono annullarsi.
Non si può dividere per zero, giusto?
Andiamo avanti facendo delle manipolazioni algebriche che puoi seguire qui sotto nella fig. 2.2:
Ora, prendiamo l' espressione della x ottenuta dalla prima equazione del sistema e la mettiamo al posto della x nella seconda equazione (metodo di sostituzione).
Puoi seguire i passaggi qui sotto nella fig. 3.2:
Andiamo avanti:
Una volta trovato il valore della y, lo mettiamo nell' espressione della x e calcoliamo:
x = (1/4)⋅y
x = (1/4)⋅8 = 2
Ti faccio notare che sia x=2 sia y=8 rispettano le C. E., dunque sono valori accettabili.
Abbiamo così trovato la soluzione del sistema assegnato:
la coppia (2, 8).
Infatti, x=2 e y=8 soddisfano entrambe le equazioni del sistema.
Verifica con dei conticini facili!
In questa esercitazione, prima di affrontare un sistema di equazioni fratte, voglio farti vedere come si calcola il determinante di una matrice quadrata 2 x 2.
Esercizio 1
Calcola il determinante della matrice quadrata, 2 x 2, che vedi qui sotto nella Fig. 1.1
 |
| Fig. 1.1 determinante di una matrice 2 x 2 |
Sui libri puoi trovare un altro modo di rappresentare il determinante di una matrice quadrata, come puoi vedere nella Fig. 2.1 qui sotto:
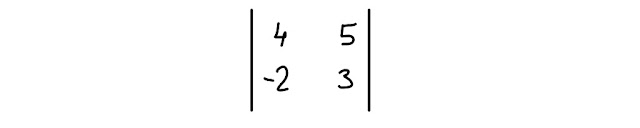 |
| Fig. 2.1 un altro modo per indicare il determinante di una matrice quadrata |
Ecco la regola:
 |
| Fig. 3.1 regola per calcolare il determinante di una matrice 2 x 2 |
La regola dice:
facciamo il prodotto tra i due elementi della prima diagonale e poi togliamo il prodotto tra i due elementi della seconda diagonale.
Qui sotto, nella Fig. 4.1, puoi vedere l' applicazione di questa semplice regola per trovare il determinante richiesto dal nostro esercizio:
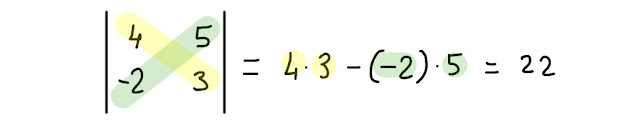 |
| Fig. 4.1 applicazione della regola per calcolare il determinante di una matrice 2 x 2 |
Esercizio 2
Risolvi questo sistema di equazioni fratte:
 |
| Fig 1.2 sistema numerico fratto assegnato |
Svolgimento Es. 2
Come prima cosa, dobbiamo controllare le condizioni di esistenza (C. E.).
Dobbiamo imporre che
y ≠ 0, x ≠ 0, y ≠ 2
Perché imponiamo queste condizioni?
Perché i denominatori presenti nel sistema non possono annullarsi.
Non si può dividere per zero, giusto?
Andiamo avanti facendo delle manipolazioni algebriche che puoi seguire qui sotto nella fig. 2.2:
 |
| Fig 2.2 manipolazioni algebriche |
Puoi seguire i passaggi qui sotto nella fig. 3.2:
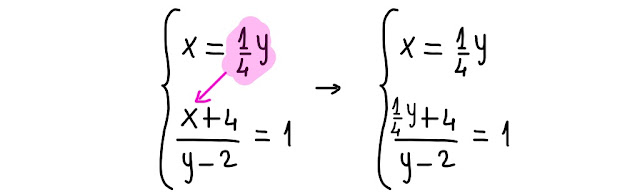 |
| Fig 3.2 ancora manipolazioni algebriche |
Andiamo avanti:
Una volta trovato il valore della y, lo mettiamo nell' espressione della x e calcoliamo:
x = (1/4)⋅y
x = (1/4)⋅8 = 2
Ti faccio notare che sia x=2 sia y=8 rispettano le C. E., dunque sono valori accettabili.
Abbiamo così trovato la soluzione del sistema assegnato:
la coppia (2, 8).
Infatti, x=2 e y=8 soddisfano entrambe le equazioni del sistema.
Verifica con dei conticini facili!
Iscriviti a:
Post (Atom)
Ti potrebbero interessare anche questi post:
-
Ultimo aggiornamento: 28 11 2019 Questa esercitazione è consultabile gratuitamente online. Se vuoi anche scaricarla in formato P...
-
Ultimo aggiornamento: 02/01/2022 Che cos' è una funzione? Come si trova il dominio di una funzione? Come si classificano le funzioni? Ci...
-
ultimo aggiornamento: 04 12 2020 Grafici e Trasformazioni Geometriche Come si disegna il grafico di una funzione applicando le trasform...
-
In questa esercitazione, estratta dal mio Tutorial sulla Parabola , vedremo lo svolgimento di 2 esercizi di matematica per le Super...
-
Qui trovi le formule per calcolare: 1) il tempo di volo di un proiettile lanciato orizzontalmente ; 2) la gittata di un proiettile spara...
-
ISCRIVITI alla nostra Newsletter per ricevere gli aggiornamenti e i contenuti speciali pensati per gli iscritti. In questo post svolg...
-
In questo post, vedremo come si disegnano(senza utilizzare il computer❗️🤓🙄😀) delle funzioni, leggermente complesse, partendo dai grafic...
-
Ho preparato un video, lo trovi qui sotto, in cui svolgo e commento 4 equazioni goniometriche lineari in seno e coseno, sfruttando il meto...
-
In questa esercitazione sulle operazioni tra polinomi , che è la n° 3 su questo argomento, vedremo come si risolvono 4 esercizi. Dico su...
-
In questa esercitazione di matematica delle Superiori , che è divisa in 3 parti, vedremo come si determina il dominio di una funzione ...
Archivio blog
-
▼
2013
(138)
-
▼
settembre
(41)
- PERCHÉ SONO IMPORTANTI LE LEZIONI PRIVATE
- TRASFORMAZIONE DEL GRAFICO DI UNA FUNZIONE
- CURIOSITÀ: simmetria e parole palindrome
- TRASFORMAZIONI GEOMETRICHE: DAL GRAFICO ALLA FUNZIONE
- calcolo del periodo di una funzione
- FUNZIONE INVERSA
- come in uno stereogramma...
- Funzioni periodiche
- Curiosità matematiche: M' ama o non m' ama?
- Introduzione informale al concetto di limite
- Esercizio sul metodo grafico per risolvere una dis...
- Esercizio di base sul fascio di circonferenze
- Esercizio di base sull' asse radicale
- Esercizio di base sulla tangente ad una circonferenza
- Ancora sulla simmetria assiale
- Esercizio su grafici e trasformazioni
- Grafici e Trasformazioni Geometriche
- L' enigma dei numeri primi
- Problema sulle trasformazioni geometriche
- Esercizio sulla omotetia
- Esercizio dimostrativo sulla rotazione
- Esercizio dimostrativo sulla simmetria assiale
- Esercizio di base sulle disequazioni in due variabili
- Esercizio di base sul fascio di rette
- Esercizio di base sul verso di rotazione delle ret...
- Esercizio di base sul fascio di rette
- Calcolo delle coordinate del baricentro di un tria...
- Esercizio di base sul coefficiente angolare
- Esercizio di base sulla retta passante per due punti
- Esercizio di base sulle parti proporzionali di un ...
- Esercizio di base sul baricentro di un triangolo
- Esercizio di base sulla simmetria centrale
- Esercizio di base sul punto medio di un segmento
- Esercizio di base sulla distanza tra due punti
- Esercizio di base sulle coordinate di un punto su ...
- Importanza delle lezioni private di matematica
- Esercizio di base sui sistemi lineari nella geometria
- CURIOSITÀ MATEMATICHE: La poesia nella solitudine ...
- Problema di base sui sistemi lineari
- Sistemi Lineari: Letterali Interi e Letterali Fratti
- Sistemi lineari numerici fratti
-
▼
settembre
(41)