Funzioni Goniometriche e Trasformazioni Geometriche

ultimo aggiornamento: 04 12 2020

Grafici e Trasformazioni Geometriche

Come si disegna il grafico di una funzione applicando le trasformazioni geometriche

Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.

Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.

In questo breve tutorial, ti propongo 4 funzioni goniometriche di cui vogliamo disegnare i grafici applicando alcune particolari

trasformazioni geometriche: dilatazioni e contrazioni

Anche se le funzioni di cui andremo a disegnare i grafici non sono particolarmente complesse, comunque ti farò vedere le regole generali per decidere che cosa fare in base alla tipologia delle funzioni assegnate in questa esercitazione.

Questa esercitazione è disponibile anche in PDF stampabile, sempre a portata di mano, consultabile tutte le volte che vuoi:

==> Sì, voglio il PDF!

Per disegnare la prima funzione proposta,

y = (⅓)⋅sin(x) ,

partiamo dalla funzione più semplice,

y = sin(x) ,

e sul suo grafico (fig. 1 qui sotto)

Fig. 1

operiamo una contrazione verticale (fig. 2 qui sotto), visto che la funzione assegnata da disegnare 

è del tipo

y = k ⋅ f(x) , k=⅓ , 0<k<1

Se la funzione è di questo tipo, allora si avrà una 

contrazione verticale 

del grafico della funzione più semplice da cui si parte, cioè una contrazione lungo l' asse y, come si può vedere nella fig. 2 qui sotto.

Fig. 2

Le coordinate del punto generico P(x,y) della funzione di partenza (quella più semplice da cui si parte) si trasformano nelle coordinate del corrispondente punto P'(x', y') della funzione assegnata secondo la seguente regola:

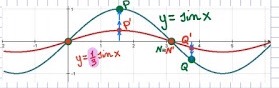
Osserviamo la fig. 2 qui sopra.

L' ascissa del punto P' rimane quella del punto P, mentre l' ordinata del punto P' diventa 1/3 dell' ordinata del punto P.

Guardiamo il punto Q che si trasforma nel punto Q':

L' ascissa del punto Q' rimane quella del punto Q, mentre l' ordinata del punto Q' diventa 1/3 dell' ordinata del punto Q.

Con questa regola, capiamo perché il punto N coincide col punto N' (N≡N'):

L' ascissa del punto N' rimane quella del punto N, mentre l' ordinata del punto N' diventa 1/3 dell' ordinata del punto N, cioè

(1/3)⋅0=0.

Prima di andare avanti, ci tengo a dirti che puoi imparare di più attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è

Matematica Quinquennio

Se vuoi scoprire come ottenere alcuni estratti gratuiti e iniziare un percorso, fai click sul link qui sotto:

iscriviti gratis qui.

Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.

Se vuoi invece ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.

Bene, torniamo agli esercizi!

Andiamo a disegnare la seconda funzione proposta,

y = sin(2⋅x)

Essa è del tipo

y = f(k⋅x) , k=2 , k>1

Se la funzione è di questo tipo, allora si avrà una 

contrazione orizzontale 

del grafico della funzione più semplice da cui si parte, cioè una contrazione lungo l' asse x, come si può vedere nella fig. 4 qui sotto.

Partiamo dalla funzione più semplice,

y = sin(x) ,

e sul suo grafico (fig. 3 qui sotto)

Fig. 3

operiamo una contrazione orizzontale, come si può vedere nel grafico della fig. 4 qui sotto:

Fig. 4

Le coordinate del punto generico P(x,y) della funzione di partenza (quella più semplice) si trasformano nelle coordinate del corrispondente punto P'(x', y') della funzione assegnata secondo la seguente regola:

 

Osserviamo la fig. 4 qui sopra:

l' ascissa del punto P', generico, è la metà dell' ascissa del punto P, mentre l' ordinata del punto P' rimane uguale all' ordinata del punto P.

Stesso discorso vale, ovviamente, per il punto Q':

la sua ascissa è la metà dell' ascissa del punto Q, mentre la sua ordinata rimane uguale all' ordinata del punto Q.

In particolare, l' ascissa del punto O' è la metà dell' ascissa del punto O, cioè (1/2)⋅0=0,  mentre l' ordinata del punto O' rimane uguale all' ordinata del punto O, cioè zero.

Ecco perché il punto O coincide col punto O' (O≡O') 

Passiamo alla terza funzione proposta,

y = 2cos(x)

Essa è del tipo

y = k⋅f(x) , k=2 , k>1

Se la funzione è di questo tipo, allora si avrà una

dilatazione verticale 

del grafico della funzione più semplice da cui si parte, cioè una dilatazione lungo l' asse y, come si può vedere nella fig. 6 qui sotto.

Partiamo dalla funzione più semplice,

y = cos(x) ,

e sul suo grafico (fig. 5 qui sotto)

Fig. 5

operiamo appunto una dilatazione lungo l' asse delle ordinate (fig. 6 qui sotto):

Fig. 6

Le coordinate del punto generico P(x,y) della funzione di partenza (quella più semplice) si trasformano nelle coordinate del corrispondente punto P'(x', y') della funzione assegnata secondo la seguente regola:

Osserviamo la fig. 6 qui sopra:

l' ascissa del punto P', generico, rimane uguale all' ascissa del punto P, mentre l' ordinata del punto P' diventa il doppio dell' ordinata del punto P.

Il punto N coincide col punto N' perché l' ascissa del punto N' rimane uguale all' ascissa del punto N (fig. 6 qui sopra), mentre l' ordinata del punto N' diventa il doppio dell' ordinata del punto N, cioè 

2⋅0=0.

Per finire, passiamo alla quarta e ultima funzione di questa esercitazione,

y = sin(x/3)

Essa è del tipo

y = f(x/k) , k=3 , k>1

Se la funzione è di questo tipo, allora si avrà una

dilatazione orizzontale 

del grafico della funzione più semplice da cui si parte, cioè una dilatazione lungo l' asse x, come si può vedere nella fig. 8 qui sotto.

Partiamo dalla funzione più semplice,

y = sin(x) ,

e sul suo grafico (fig. 7 qui sotto)

Fig. 7

operiamo  appunto una dilatazione lungo l' asse x (fig. 8 qui sotto):

Fig. 8

Le coordinate del punto generico P(x,y) della funzione di partenza (quella più semplice) si trasformano nelle coordinate del corrispondente punto P'(x', y') della funzione assegnata secondo la seguente regola:

Osserviamo la fig. 8 qui sopra:

l' ascissa del punto P', generico, diventa il triplo dell' ascissa del punto P, mentre l' ordinata del punto P' rimane uguale all' ordinata del punto P.

Bene! Dovrebbe, a questo punto, essere chiaro per quale motivo il punto O coincide col punto O' 

😉

Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto: 

troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.

Alla prossima lezione. Ciao, ti aspetto!

Puoi guardare questa esercitazione nel video qui sotto: