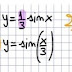In questa esercitazione vedremo 4 quesiti di matematica svolti(si tratta di una mia rielaborazione), assegnati agli studenti chiamati ad affrontare la prova scritta dell' esame di maturità del liceo scientifico, qualche anno fa.
La mia nuova versione di questi esercizi di matematica svolti punta a migliorare la fruibilità dei contenuti.
Qui troverai:
• un quesito di trigonometria;
• uno sulla formula binomiale di Newton;
• uno sul calcolo combinatorio e delle probabilità;
• l' ultimo quesito è sul minimo relativo di una funzione.
Permettimi di darti un duplice consiglio:
1) cerca sempre di affrontare autonomamente, almeno nella prima fase, i problemi di matematica, contando soltanto sulle tue forze, perchè così è possibile trovare soluzioni e metodi originali;
2) dopo il lavoro individuale, nella seconda fase, se ti è possibile, dovresti cercare di rivedere gli stessi problemi confrontandoti o collaborando con altre persone(compagni, amici, colleghi, insegnanti etc.), per condividere con loro il tuo lavoro e vedere punti di vista e metodi differenti.
Se non riesci a risolvere il problema nella prima fase, nello step successivo hai una buona occasione per chiedere ad altre persone l' aiuto di cui hai bisogno.
Io sono qui per aiutarti!! 😊
Scrivi ✎ nei commenti qui sotto cosa pensi di questo consiglio che ti ho dato.
Per risolvere questo quesito, applichiamo il teorema dei seni:
α ≅ 41,81°
α ≅ 41° + 0,81°
Sappiamo che 1° = 60' (un grado è fatto di sessanta primi), quindi
0,81° = 0,81⋅1° = 0,81⋅60' = 48,6' (48,6 primi).
Ecco, poichè il quesito ci chiede di esprimere l' angolo α in gradi e primi sessagesimali, possiamo fermarci scrivendo che
α ≅ 41° 48,6'.
A questo punto, permettimi di andare un pò oltre.
Aspetta un attimo! Hai fatto l' iscrizione gratuita al mio Canale Youtube?
👇👇👇
α ≅ 41° 48' + 0,6'
Sappiamo anche che 1' = 60'' (un primo è fatto di sessanta secondi), dunque
0,6' = 0,6⋅1' = 0,6⋅60'' = 36'' (36 secondi).
Per esprimere l' angolo coinvolgendo anche i secondi, possiamo scrivere così:
41,81° =
= 41° + 0,81° =
= 41° + 48,6' =
= 41° + 48' + 0,6' =
= 41° + 48' + 36''
che per semplicità riscriviamo nel seguente modo:
41° 48' 36'' .
Se hai domande, dubbi, osservazioni, metodi alternativi a quello che ti ho mostrato, ti prego di farmelo sapere ✎ nei commenti qui sotto. Purtroppo non prenderò in considerazione i commenti anonimi☹️.
 |
| ISCRIVITI GRATIS seguendo questo link |
Passiamo al 2° quesito.
Ecco il testo:
Nel nostro caso particolare abbiamo che
A = 2a² , B = -3b³ .
Poniamo adesso il generico termine della sommatoria( ∑ ) uguale al valore indicato dal quesito:
Applicando le proprietà delle potenze e ordinando l' espressione, si ha:
Osserviamo.
Per avere 9 come esponente di b, dobbiamo scegliere
k = 3 (3k = 9 → k = 3);
l' esponente di a, cioè 2(n-k), deve essere posto uguale a 4, come indica il quesito proposto.
Dunque, poichè k = 3, abbiamo
2(n-3) = 4 → n = 5 .
Basta adesso verificare che la parte evidenziata in verde valga -1080:
Proprio così, rimane da calcolare 2⋅5⋅4⋅(-27), che fa esattamente -1080.
Quindi il valore di n è 5 😊
Se hai domande, dubbi, osservazioni, metodi alternativi a quello che ti ho mostrato, ti prego di farmelo sapere ✎ nei commenti qui sotto. Purtroppo non prenderò in considerazione i commenti anonimi☹️.
Se hai domande, dubbi, osservazioni, metodi alternativi a quello che ti ho mostrato, ti prego di farmelo sapere ✎ nei commenti qui sotto. Purtroppo non prenderò in considerazione i commenti anonimi☹️.
Prima di passare al terzo quesito, ti ricordo che è ammessa alla Seconda Prova dell' Esame di Stato del Liceo Scientifico la Calcolatrice Grafica senza Calcolo Simbolico.
Ti suggerisco questa Calcolatrice Grafica senza Calcolo Simbolico. 🚀🚀🚀
💛 Fai clic sul Pulsante Donazione e aiutaci a realizzare nuove lezioni GRATUITE 💛 Grazie!!! 😊
Terzo quesito di questo post:
Tutte le possibili uscite, cioè tutte le possibili terne, sono, applicando il metodo delle possibilità,
6⋅6⋅6 = 216.
Questo è vero perchè ciascun dado può dare 1 oppure 2 oppure 3 oppure 4 oppure 5 oppure 6 (6 possibilità).
Poichè abbiamo a che fare con 3 dadi, tutte le possibili terne sono proprio 6⋅6⋅6 = 216.
⬜ ⬜ ⬜ (i 3 dadi 😊, ciascuno con 6 possibilità: 1, 2,...,6)
6 ⋅ 6 ⋅ 6 = 216
Vediamo ora le terne di numeri che danno 9 come somma:
x + y + z = 9.
Sfruttiamo le rappresentazioni ad albero:
Contando i casi favorevoli, cioè il numero delle uscite in cui la somma dei tre numeri è 9 ( x + y + z = 9 ), otteniamo 25.
Qual è invece il numero dei casi possibili?
Il numero dei casi possibili è dato dal numero di tutte le terne possibili, cioè di tutte le uscite possibili.
Lo abbiamo già calcolato: esso vale 216.
Dunque, la probabilità che esca una terna di numeri la cui somma è uguale a 9 è data dal rapporto tra il numero dei casi favorevoli e il numero dei casi possibili:
25
—— ≅ 0,11
216
Osserviamo adesso la prossima rappresentazione ad albero per vedere quante sono le terne di numeri la cui somma è 10:
x + y + z = 10
Osserviamo adesso la prossima rappresentazione ad albero per vedere quante sono le terne di numeri la cui somma è 10:
x + y + z = 10
Noti la differenza tra questa "griglia" e la precedente?
Contando i casi favorevoli, cioè il numero delle uscite in cui, questa volta, la somma dei tre numeri è 10 ( x + y + z = 10 ), otteniamo 27.
Dunque, la probabilità che esca una terna di numeri la cui somma è uguale a 10 è data dal rapporto tra il numero dei casi favorevoli e il numero dei casi possibili:
27
—— ≅ 0,12
216
Per concludere, poichè 0,12 > 0,11, possiamo affermare che è più probabile vincere se si scommette sull' uscita di una terna di numeri la cui somma vale 10.
Se hai domande, dubbi, osservazioni, metodi alternativi a quello che ti ho mostrato, ti prego di farmelo sapere ✎ nei commenti qui sotto. Purtroppo non prenderò in considerazione i commenti anonimi☹️.
Andiamo al quarto e ultimo quesito di questa esercitazione.
Per concludere, poichè 0,12 > 0,11, possiamo affermare che è più probabile vincere se si scommette sull' uscita di una terna di numeri la cui somma vale 10.
Se hai domande, dubbi, osservazioni, metodi alternativi a quello che ti ho mostrato, ti prego di farmelo sapere ✎ nei commenti qui sotto. Purtroppo non prenderò in considerazione i commenti anonimi☹️.
Andiamo al quarto e ultimo quesito di questa esercitazione.
Ecco il testo:
Studiamo graficamente la disequazione che viene dal porre
f '(x) ≥ 0.
ln(x) - x + 2 ≥ 0 ⟶ ln(x) ≥ x - 2 .
A questo punto, disegniamo il diagramma di y = ln(x) e quello di
y = x - 2, chiedendoci dove il grafico della funzione logaritmica sta sopra o interseca ( ≥ ) il grafico della retta.
Guardando il grafico, possiamo affermare che la derivata prima della funzione f è maggiore o uguale a zero ( y ' ≥ 0 ) per
x₁ ≤ x ≤ x₂.
Visualizziamo dove la funzione è crescente e dove è decrescente:
Si ha un punto di minimo relativo in corrispondenza di x₁, e, siccome è compreso tra 0 e 1, la risposta esatta è la
(D) x₁ = 0,159.
Se hai domande, dubbi, osservazioni, metodi alternativi a quello che ti ho mostrato, ti prego di farmelo sapere ✎ nei commenti qui sotto. Purtroppo non prenderò in considerazione i commenti anonimi☹️.
Se hai trovato utile questa esercitazione e vuoi sostenere questo mio progetto didattico, puoi iscriverti al mio canale Youtube, condividere questa lezione sui tuoi Social preferiti, sfruttando i pulsanti dedicati, e puoi anche fare una donazione. Grazie!!☺️
Follow me 😊, per ricevere gli aggiornamenti, le curiosità e altro ancora direttamente sui tuoi Social preferiti(ci vediamo anche lì, ti aspetto! 😉👋):
👇👇👇
Instagram (clic), YouTube (clic), Linkedin (clic)
Facebook (clic), Google+ (clic), Twitter (clic)