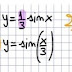Moto parabolico con lancio in direzione obliqua

Diamo un pò di formule:

Moto Parabolico con lancio orizzontale

Qui trovi le formule per calcolare:

1) il tempo di volo di un proiettile lanciato orizzontalmente;

2) la gittata di un proiettile sparato lungo l' orizzontale;

3) l' equazione della traiettoria parabolica di un proiettile lanciato con una velocità iniziale orizzontale.

Diamo un po' di formule:

Per lo studio completo della teoria, ti suggerisco questo libro.

Prima di passare all' equazione della traiettoria parabolica, follow me 😊 per ricevere gli aggiornamenti, le curiosità e altro ancora direttamente sui tuoi Social preferiti(ci vediamo anche lì, ti aspetto! 😉👋):
👇👇👇

Instagram (clic), YouTube (clic), Linkedin (clic)

Facebook (clic), Google+ (clic), Twitter (clic)

Il Grafico delle Funzioni e le Trasformazioni Geometriche (2^ Parte)

In questo post (2^ parte), vedremo come si disegnano(senza utilizzare il computer❗️🤓🙄😀) delle funzioni, leggermente complesse, partendo dai grafici di funzioni più semplici e sfruttando le trasformazioni geometriche, in particolare le dilatazioni e le contrazioni. 

Il mio scopo è quello di mostrarti alcuni passi fondamentali attraverso lo svolgimento di esercizi di base.

Puoi accedere alla 1^ parte facendo clic qui.

Il perchè 🔍 delle trasformazioni che sto per mostrarti sarà trattato in un altro mio elaborato.

Poichè lo studio approfondito della teoria è fondamentale per affrontare bene gli esercizi e i problemi di Matematica, ti consiglio dei libri validi, per studiare i concetti teorici basilari legati alle trasformazioni geometriche, che puoi ottenere grazie a dei link che ti ho fornito in fondo a questo post.

Come abbiamo fatto nella 1^ parte, anche qui facciamo degli schemi relativi alle trasformazioni geometriche applicate ai grafici delle funzioni che ci rimangono da trattare.

Schema 1

Facciamo subito un' applicazione.

Vogliamo disegnare la funzione y = ( x/3 )² + ( x/3 ) - 2.

Essa proviene dalla funzione y = x² + x - 2, dove al posto di x abbiamo messo x/3.

Siamo nel caso dello schema 1, perchè

f(x) = x² + x - 2   e
f(x/3) = ( x/3 )² + ( x/3 ) - 2, in cui k=3.

Ora, poichè k > 1, si ha che il grafico di y = f(x/3) = ( x/3 )² + ( x/3 ) - 2 si ottiene dilatando (fig. 1), lungo l' asse x, il grafico della funzione più semplice, y = f(x) = x² + x - 2.

Vediamolo con un disegno:

Fig. 1

Nella Fig. 1 si vede che il punto A si trasforma nel punto A', il punto B viene trasformato nel punto B', e così via.

In pratica, l' ascissa del generico punto della funzione blu viene moltiplicata per 3 (il nostro k) per ottenere l' ascissa del punto corrispondente della funzione rossa.

In altre parole, prendo l' ascissa di A (x=-2) e la moltiplico per k=3 per ottenere l' ascissa del suo punto corrispondente A' ( x' = 3(-2) = -6 ). E così si fa di tutti gli altri punti più significativi, come il punto B che si trasforma nel punto B' e il vertice V che si trasforma nel vertice V'.

Adesso vogliamo disegnare la funzione y = ( 3x )² + ( 3x ) - 2.

Essa proviene dalla funzione y = x² + x - 2, dove al posto di x abbiamo messo 3x.

Notiamo che

Siamo sempre nel caso dello schema 1, perchè

f(x) = x² + x - 2   e

in cui k=1/3.

Ora, poichè 0 < k < 1, si ha che il grafico di y = f(3x) = ( 3x )² + ( 3x ) - 2 si ottiene contraendo (fig. 2), lungo l' asse x, il grafico della funzione più semplice, y = f(x) = x² + x - 2.

Vediamolo con un disegno:

Fig. 2

In pratica, l' ascissa del punto generico P di y = f(x) = x² + x - 2 viene divisa per 3 per ottenere l' ascissa del punto corrispondente P' di y = f(3x) = ( 3x )² + ( 3x ) - 2.

Puoi trovare i miei e-Books qui


Ah, dimenticavo ☺,

Follow me 😊, per ricevere gli aggiornamenti, le curiosità e altro ancora direttamente sui tuoi Social preferiti(ci vediamo anche lì, ti aspetto! 😉👋):
👇👇👇

Instagram (clic), YouTube (clic), Linkedin (clic)

Facebook (clic), Google+ (clic), Twitter (clic)


Passiamo a questo punto allo schema relativo alla contrazione/dilatazione verticale.

Schema 2

Vogliamo disegnare il grafico della funzione y = 3(x² + x - 2).

Lo schema 2 ci dice che dobbiamo dilatare verticalmente, k = 3 > 1, il diagramma di y = x² + x - 2.

Vediamo il disegno qui sotto:

Fig. 3

In pratica, l' ordinata del punto P generico di y = x² + x - 2 viene moltiplicata per k=3 per ottenere l' ordinata del punto corrispondente P' della funzione y = 3( x² + x - 2 ).

V si trasforma, secondo questa dilatazione verticale, in V'; P diventa P', e così via.

Prenditi ora qualche istante per condividere questo Blog su Facebook facendo clic sui bottoni qui sotto. Grazie!! ;-)

Ti potrebbero interessare altri esercizi svolti che si trovano in questa pagina nella sezione dedicata alle trasformazioni geometriche, oppure guarda questo mio video:

Per quanto riguarda il grafico di y = (1/3)(x² + x - 2), abbiamo che k = 1/3 è compreso tra 0 e 1, e dunque dobbiamo contrarre verticalmente il diagramma di y = x² + x - 2, come mostrato nella figura qui sotto:

In pratica, cosa succede all' ordinata del generico punto P della funzione y = x² + x - 2 per trasformarsi nel suo corrispondente punto P' della funzione y = (1/3)(x² + x - 2) ?
Puoi rispondere nei commenti qui sotto👇

Inoltre, ho pubblicato un mio eBook in cui svolgo e commento ben 13 esercizi, più sostanziosi di quelli trattati in questo post, proprio sulle trasformazioni geometriche applicate ai grafici di funzioni.

Se credi che questi contenuti siano validi per te e per alcune persone che conosci, condividi questo post sui tuoi Social preferiti, sfruttando i pulsanti che trovi in fondo a questo mio elaborato, e iscriviti al mio Canale YouTube:
👇👇👇

Come dicevo all' inizio di questo post, data l' importanza di studiare bene i concetti di matematica, ti consiglio vivamente di approfondire la teoria, relativa a questi argomenti, sul libro che puoi ottenere grazie al link che trovi qui sotto 👇👇👇 📚:

Matematica per le Scuole superiori, con e-book ed espansione online(vol 4)


Puoi avere anche gli altri volumi. Ecco i link:

Matematica: Algebra, Geometria e Statistica. Per le Scuole Superiori, con espansione online(vol 1)

Matematica: Algebra, Geometria e Probabilità. Per le Scuole superiori, con espansione online(vol 2)

Matematica per le Scuole superiori, con Maths in english ed espansione online e DVD-ROM(vol 3)

Matematica per le Scuole superiori, con e-book ed espansione online(vol 5)

Principio di Induzione: come si applica nelle dimostrazioni

Vuoi imparare il Principio di Induzione e come si applica nelle dimostrazioni in matematica?

Nel mio book dedicato agli

esercizi svolti sul Principio di Induzione,

trovi diversi esercizi, accuratamente selezionati, che ti mostrano

come si applica il Principio di Induzione

in modo pratico e chiaro.

Passa all' azione: metti le mani sulla tua copia e iniziamo a studiare insieme!

Il Grafico delle Funzioni e le Trasformazioni Geometriche (1^ Parte)

In questo post, vedremo come si disegnano(senza utilizzare il computer❗️🤓🙄😀) delle funzioni, leggermente complesse, partendo dai grafici di funzioni più semplici e sfruttando le trasformazioni geometriche.

Il perchè 🔍 delle trasformazioni che sto per mostrarti sarà trattato in un altro mio elaborato.

Poichè lo studio approfondito della teoria è fondamentale per affrontare bene gli esercizi e i problemi di Matematica, ti consiglio dei libri validi, per studiare i concetti teorici basilari legati alle trasformazioni geometriche, che puoi ottenere grazie a dei link che ti ho fornito in fondo a questo post.

Disegnare il grafico di questa funzione:

Seguimi su Instagram, Youtube, Facebook ecc. Utilizza i bottoni qui sotto:

Ricorriamo al seguente schema, in cui k rappresenta un numero reale (k ∈ ℝ):

Schema 1

La nostra f(x) è ln(x).

f(x)=ln(x).

Dobbiamo disegnare f(x+k)=ln[x+(-2)].

k= -2 

Dunque, poichè k= -2 < 0 , il grafico che dovremo disegnare sarà quello di ln(x) traslato lungo la direzione dell' asse x con spostamento |-2 |= 2 verso destra.

Ecco il disegno:

Fig. 1

Ti faccio notare che oltre alla traslazione del diagramma di ln(x), assistiamo anche alla traslazione dell' asintoto verticale:

l' asse di equazione x=0 ( asse y, asintoto verticale di ln(x) ) viene traslato verso destra lungo la direzione dell' asse delle ascisse con uno spostamento pari a 2, diventando così l' asintoto verticale(x=2) della funzione ln(x-2).

Adesso ti fornisco altri schemi grazie ai quali potrai disegnare i grafici di alcune funzioni assegnate, leggermente complesse, dopo avere applicato certe trasformazioni geometriche a funzioni più semplici di equazione y=f(x).

Schema 2

Facciamo subito un esempio per applicare la traslazione parallela all' asse y dello schema 2.

Vogliamo disegnare la seguente funzione:

y = x² + x - 2 ,

che possiamo vedere, giusto per "giocare" con le trasformazioni geometriche, come 

y = ( x² + x ) - 2 ,

in cui f(x) = ( x² + x ) e k = -2 .

Cosa dice lo schema 2 ?

Dobbiamo traslare il grafico di f(x) lungo l' asse y, spostandolo di |-2|=2 verso il basso.

Il grafico di f(x) è la seguente parabola, y = x² + x :

Fig. 2

che traslata verso il basso, di 2, diventa y = ( x² + x ) - 2 :

Fig. 3

Ecco lo schema 3:

Schema 3

Facciamo subito un esempio per applicare la trasformazione geometrica dello schema 3.

Vogliamo disegnare la seguente funzione:

y = (-x)² + (-x) - 2 

Essa proviene dalla funzione y = f(x) = x² + x - 2, se al posto di x mettiamo -x.

Cosa dice lo schema 3 ?

Che il grafico di y = f(-x) =(-x)² + (-x) - 2 è il simmetrico del grafico di y = f(x) = x² + x - 2 rispetto all' asse y.

Di quest' ultima funzione conosciamo già il diagramma (fig. 4).

Fig. 4

Disegnando il simmetrico del grafico di Fig. 4 rispetto all' asse y, si ottiene

Fig. 5

Il grafico della funzione  y = f(-x) =(-x)² + (-x) - 2  è quello che passa per i punti M', Q' e P'.

In pratica, non facciamo altro che disegnare i simmetrici rispetto all' asse y dei punti della f(x) = x² + x - 2, come, ad esempio, P, Q ed M.

Nella fig. 5 puoi vedere che P si trasforma in P', Q si trasforma in Q'(ma coincidono!), M si trasforma in M', e così via.

Adesso lavoriamo sulla trasformazione geometrica del prossimo schema, il 4°.

Schema 4

Vogliamo disegnare y = - ( x² + x - 2 ) .

f(x) = x² + x - 2 è una nostra vecchia conoscenza 😄, e dobbiamo disegnare y = - f(x).

Cosa dice lo schema 4 ?

Dobbiamo rappresentare il simmetrico del grafico di y = f(x) = x² + x - 2 rispetto all' asse x per ottenere il grafico della funzione y = - ( x² + x - 2 ).

Nella Fig. 6 qui sotto, partendo dal diagramma di y = f(x) e "simmetrizzandolo" rispetto all' asse x, riusciamo a disegnare il grafico di y = - f(x) :

Fig. 6

Se non ti sono chiari alcuni passaggi, lascia qualche commento nella sezione qui sotto, e cercheremo di risponderti 👍.

Adesso, grazie allo schema 5, disegneremo il grafico della funzione  y = f(|x|) = |x|² + |x| - 2, partendo dalla nostra solita vecchia conoscenza, y = f(x) = x² + x - 2 .

Schema 5

Cosa dice lo schema 5?

Dobbiamo considerare la porzione destra (quella che giace nel semipiano delle ascisse positive) del grafico di y = f(x) = x² + x - 2 e unirla alla simmetrica di questa porzione destra rispetto all' asse y.

Nella Fig. 7 qui sotto si vede il grafico blu della y = f(x) = x² + x - 2, indicato dalle tante freccettine rosse, sul quale viene evidenziata in viola la porzione che sta a destra dell' asse y, la quale viene unita con la sua simmetrica rispetto all' asse delle ordinate per ottenere il diagramma di y = f(|x|) = |x|² + |x| - 2.

Fig. 7

In conclusione, nella fig. 8 qui sotto vediamo che occorre non tenere conto del ramo blu che sta a sinistra dell' asse y e tenere i rami disegnati in viola.

Fig. 8

Prima di continuare, ti ricordo che puoi trovare qui il mio eBook completo sui Monomi, con tanti ricchi esercizi svolti.

E qui puoi trovare il mio eBook sul Principio di Induzione, con diversi esercizi svolti.

Inoltre, ho pubblicato un mio eBook in cui svolgo e commento ben 13 esercizi, più sostanziosi di quelli trattati in questo post, proprio sulle trasformazioni geometriche applicate ai grafici di funzioni.

Grazie allo schema 6, riusciamo a disegnare il grafico di y = |f(x)| = |x² + x - 2|, partendo dal grafico di y = f(x) = x² + x - 2.

Cosa dice lo schema 6 ?

Schema 6

Dunque, osservando la fig. 9, del grafico della funzione y = f(x) = x² + x - 2 si tengono i rami positivi (quelli che stanno al di sopra dell' asse x) e a essi uniamo la porzione negativa (quella che sta sotto l' asse delle ascisse) simmetrizzata rispetto all' asse orizzontale.

Quello che si ottiene (fig. 9 qui sotto) è il grafico verde della funzione y = |f(x)| = |x² + x - 2|

Fig.9

Qui trovi la 2^ parte dedicata alle contrazioni e dilatazioni dei grafici.

Se credi che questi contenuti siano validi per te e per alcune persone che conosci, condividi questo post sui tuoi Social preferiti, sfruttando i pulsanti che trovi in fondo a questo mio elaborato, e iscriviti al mio Canale YouTube:

👇👇👇

Scopri come ottenere il mio eBook in cui svolgo e commento ben 13 esercizi, più sostanziosi di quelli trattati in questo post, proprio sulle trasformazioni geometriche applicate ai grafici di funzioni.

Prova a disegnare (senza utilizzare il computer❗️🤓🙄😀) le funzioni riportate qui sotto, partendo dai grafici di funzioni più semplici e sfruttando le trasformazioni geometriche.

Fammi sapere nella sezione dei commenti come svolgi questi esercizi. Buon lavoro!

Interessante sarà vedere anche come rappresentare graficamente una funzione come questa:

Come dicevo all' inizio di questo post, data l' importanza di studiare bene i concetti di matematica, ti consiglio vivamente di approfondire la teoria, relativa a questi argomenti, sui libri che puoi ottenere grazie ai link che trovi qui sotto 👇👇👇 📚:

Matematica: Algebra, Geometria e Probabilità. Per le Scuole superiori, con espansione online(vol 2)
Matematica per le Scuole superiori, con e-book ed espansione online(vol 4)


Puoi avere anche gli altri volumi. Ecco i link:

Matematica: Algebra, Geometria e Statistica. Per le Scuole Superiori, con espansione online(vol 1)
Matematica per le Scuole superiori, con Maths in english ed espansione online e DVD-ROM(vol 3)
Matematica per le Scuole superiori, con e-book ed espansione online(vol 5)