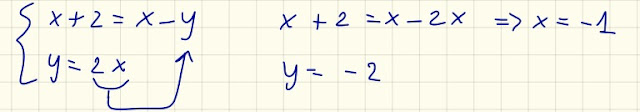Guarda questo brevissimo video:
Cerca nel blog
venerdì 28 febbraio 2014
giovedì 27 febbraio 2014
PROBLEMA DI MINIMO, SVOLTO E COMMENTATO
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Ti propongo un problema di minimo sulla geometria piana. Lo puoi scaricare da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Ti propongo un problema di minimo sulla geometria piana. Lo puoi scaricare da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO SVOLTO SUGLI ASINTOTI VERTICALI E ORIZZONTALI
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Segui @ilmatematto
Per poter trovare gli asintoti di una funzione, occorre individuare bene gli estremi finiti e infiniti (se ci sono) del campo di esistenza. Un esercizio può essere scaricato da QUI e ti illustrerà il procedimento.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Segui @ilmatematto
Per poter trovare gli asintoti di una funzione, occorre individuare bene gli estremi finiti e infiniti (se ci sono) del campo di esistenza. Un esercizio può essere scaricato da QUI e ti illustrerà il procedimento.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Tags, etichette:
asintoti orizzontali,
asintoti verticali,
come trovare asintoti funzione,
esercizi risolti asintoti,
esercizi svolti asintoti funzione
mercoledì 26 febbraio 2014
ESERCIZIO SUI MASSIMI, MINIMI E FLESSI, SFRUTTANDO LE DEFINIZIONI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio svolto può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio svolto può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO SVOLTO SUI MASSIMI E MINIMI ASSOLUTI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Ti propongo un esercizio, che sfrutta la definizione, scaricabile da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Ti propongo un esercizio, che sfrutta la definizione, scaricabile da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO RISOLTO SUI MASSIMI, MINIMI E FLESSI (METODO DELLE DERIVATE SUCCESSIVE)
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Voglio insistere sul metodo delle derivate successive per determinare i massimi, minimi e flessi perchè le idee che stanno alla base sono molto istruttive e vale la pena spendere un po' di tempo in più su questo argomento.
Un esercizio interessante può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
martedì 25 febbraio 2014
ESERCIZIO SUI PUNTI DI FLESSO (METODO DELLE DERIVATE SUCCESSIVE)
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Il metodo delle derivate successive è interessante ed è a volte trascurato. Ti propongo un esercizio che puoi scaricare da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Il metodo delle derivate successive è interessante ed è a volte trascurato. Ti propongo un esercizio che puoi scaricare da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
lunedì 24 febbraio 2014
ESERCIZIO SVOLTO SUI FLESSI (METODO DELLE DERIVATE SUCCESSIVE)
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio che mostra il metodo delle derivate successive per determinare i flessi di una funzione può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio che mostra il metodo delle derivate successive per determinare i flessi di una funzione può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO SVOLTO SUI MASSIMI, MINIMI E FLESSI COL METODO DELLE DERIVATE SUCCESSIVE
Segui @ilmatematto
Per le tue Lezioni Private di Matematica a Grosseto(con metodo INNOVATIVO ed ECONOMICO), inviami un' e-mail all' indirizzo giusemath@gmail.com
Il metodo delle derivate successive per trovare i massimi, i minimi e i flessi è stato adottato per risolvere l' esercizio che puoi scaricare da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Tags, etichette:
esercizi risolti massimo minimo,
esercizi svolti metodo derivate successive,
flessi,
massimi,
metodo derivate successive,
minimi,
punti massimo minimo flesso
domenica 23 febbraio 2014
ESERCIZIO SVOLTO SULLE EQUAZIONI DI II GRADO NELL' INSIEME DEI NUMERI COMPLESSI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
L' equazione che ti propongo ha coefficienti complessi ed è di II grado.
L' esercizio può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
L' equazione che ti propongo ha coefficienti complessi ed è di II grado.
L' esercizio può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO SVOLTO SULLA FORMA ESPONENZIALE DEI NUMERI COMPLESSI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio di base che mostra come convertire un numero complesso nella sua forma esponenziale può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio di base che mostra come convertire un numero complesso nella sua forma esponenziale può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Tags, etichette:
esercizi svolti numeri complessi,
forma esponenziale numeri complessi,
numeri complessi,
numeri complessi rappresentazione esponenziale
venerdì 21 febbraio 2014
ESERCIZIO SVOLTO SUI NUMERI COMPLESSI (OPERAZIONI)
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio di base può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio di base può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
mercoledì 19 febbraio 2014
ESERCIZIO SVOLTO SUI NUMERI COMPLESSI: RADICE N-ESIMA DELL' UNITÀ
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un interessante esercizio può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un interessante esercizio può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO RISOLTO SULLE OPERAZIONI TRA NUMERI COMPLESSI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio di base può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio di base può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
martedì 18 febbraio 2014
ESERCIZIO SVOLTO SULLA RAPPRESENTAZIONE GONIOMETRICA DI UN NUMERO COMPLESSO
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio di base che mostra come si scrive un numero complesso nella sua forma trigonometrica può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio di base che mostra come si scrive un numero complesso nella sua forma trigonometrica può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Tags, etichette:
esercizi svolti numeri complessi,
numeri complessi,
numero complesso forma goniometrica,
rappresentazione goniometrica dei numeri complessi
ESERCIZIO SVOLTO SUI MASSIMI E MINIMI IN FUNZIONI CON PARAMETRI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio interessante sui massimi e minimi di funzioni con parametri può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio interessante sui massimi e minimi di funzioni con parametri può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
lunedì 17 febbraio 2014
ESERCIZIO SVOLTO SULLE EQUAZIONI (METODO GRAFICO)
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Puoi scaricare un esercizio svolto che utilizza l' approccio grafico facendo clic QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT.
Puoi scaricare un esercizio svolto che utilizza l' approccio grafico facendo clic QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT.
Calcolo Differenziale: come si applica il Teorema di Rolle
Ultimo aggiornamento: 1/3/2021
In questa esercitazione, vedremo
Esercizio
come si applica il Teorema di Rolle.
Si dimostri che il grafico della funzione
y=f(x)=x⁵+x³+1
interseca l' asse delle ascisse in un solo punto.
Faremo una
dimostrazione per assurdo.
Tags, etichette:
applicazione teorema di Rolle,
come si applica il teorema Rolle,
dimostrazione per assurdo,
teorema Rolle,
teorema Rolle esercizi svolti
domenica 16 febbraio 2014
PROBLEMA SVOLTO COL DIFFERENZIALE DI UNA FUNZIONE
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un interessante problemino di geometria solida risolto utilizzando il differenziale di una funzione può essere scaricato da QUI.
AVVISO: visita anche l' altro sito, MATEMATECA.IT
Un interessante problemino di geometria solida risolto utilizzando il differenziale di una funzione può essere scaricato da QUI.
AVVISO: visita anche l' altro sito, MATEMATECA.IT
ESERCIZIO SVOLTO SUL DIFFERENZIALE DI UNA FUNZIONE
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Puoi scaricare un esercizio di base sul differenziale facendo clic QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Puoi scaricare un esercizio di base sul differenziale facendo clic QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
venerdì 14 febbraio 2014
ESERCIZIO SVOLTO SUL DIFFERENZIALE DI UNA FUNZIONE
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un interessante esercizio che mostra l' utilità pratica del differenziale di una funzione può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un interessante esercizio che mostra l' utilità pratica del differenziale di una funzione può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
giovedì 13 febbraio 2014
STUDIARE MATEMATICA
Ho per te un breve e importante consiglio su come studiare la matematica:
volere risolvere esercizi e problemi di matematica senza studiare bene la teoria è come volere imparare l' inglese senza studiare bene la sua grammatica.
Se non vuoi arrampicarti sugli specchi, quando provi a risolvere un quesito di matematica, allora studia bene la teoria e gli esempi della sua applicazione.
Buono studio!!
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
volere risolvere esercizi e problemi di matematica senza studiare bene la teoria è come volere imparare l' inglese senza studiare bene la sua grammatica.
Se non vuoi arrampicarti sugli specchi, quando provi a risolvere un quesito di matematica, allora studia bene la teoria e gli esempi della sua applicazione.
Buono studio!!
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
ESERCIZIO SVOLTO SUL TEOREMA DI CAUCHY
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un' applicazione del teorema di Cauchy può essere vista scaricando un esercizio da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un' applicazione del teorema di Cauchy può essere vista scaricando un esercizio da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO SVOLTO SUL TEOREMA DI CAUCHY
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Puoi scaricare un esercizio sul teorema di Cauchy facendo clic QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Puoi scaricare un esercizio sul teorema di Cauchy facendo clic QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
martedì 11 febbraio 2014
ESERCIZIO SVOLTO SUGLI INTEGRALI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
L' integrazione per parti è una tecnica che puoi vedere nell' esercizio scaricabile da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
L' integrazione per parti è una tecnica che puoi vedere nell' esercizio scaricabile da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
ESERCIZIO SVOLTO SUGLI INTEGRALI INDEFINITI
IMPORTANTE : prima di scaricare l' esercizio, sostieni questo blog di matematica GRATUITA cliccando su "MI PIACE". Grazie!!
Un esercizio che mostra una tecnica di integrazione può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
Un esercizio che mostra una tecnica di integrazione può essere scaricato da QUI.
AVVISO: visita anche l' altro mio sito, MATEMATECA.IT
lunedì 10 febbraio 2014
Numeri Complessi: Potenze dell' Unità Immaginaria
Ultimo Aggiornamento: 13/04/2020
Come si calcolano le potenze dell' unità immaginaria?
Quanto fa iⁿ, dove i è l' unità immaginaria ed n è un numero naturale?
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 espressioni che contengono potenze dell' unità immaginaria.
Esercizio 1
Calcola le seguenti espressioni:
In questo tutorial, ti voglio mostrare una tecnica di calcolo alternativa a quella proposta da alcuni manuali di matematica.
Anziché dividere l' esponente n per 4 (come probabilmente hai visto in classe o sul manuale di matematica), dividiamo per 2.
Vediamo perché:
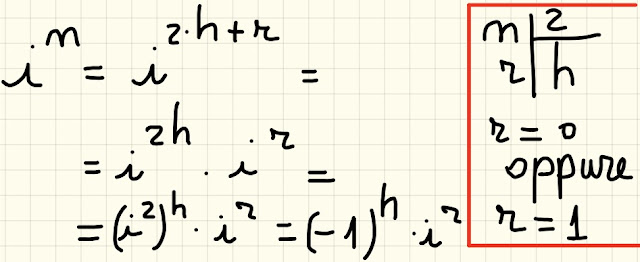 |
| Fig. 2 |
h è il quoziente della divisione dell' esponente n per 2 ed r è il resto, che può valere 0 (se n è pari) oppure 1 (se n è dispari).
Seguendo nella fig. 2 l' applicazione delle proprietà delle potenze, si arriva in fondo e si scopre che
iⁿ = (-1)ᵸ ⋅ i⁰ =
= (-1)ᵸ ⋅ 1 =
= (-1)ᵸ (se n è pari)
oppure
iⁿ = (-1)ᵸ ⋅ i¹ =
= (-1)ᵸ ⋅ i (se n è dispari)
Quindi
se n è pari,
iⁿ = -1 (se il quoziente h della divisione di n per 2 è dispari)
oppure
iⁿ = 1 (se il quoziente h della divisione di n per 2 è pari)
-------------------------------------------
se n è dispari,
iⁿ = -i (se il quoziente h della divisione di n per 2 è dispari)
oppure
iⁿ = i (se il quoziente h della divisione di n per 2 è pari)
Potenze dell' unità immaginaria
Dopo aver fatto queste considerazioni sulla potenza iⁿ di carattere generale, affrontiamo le espressioni assegnate.
1)
Calcoliamo le singole potenze in gioco:
i³¹=-i
perché 31 è dispari,
i³¹ = -i (il quoziente 15 della divisione di 31 per 2 è dispari)
-------------------------------------------
i³⁹=-i
perché 39 è dispari,
i³⁹ = -i (il quoziente 19 della divisione di 39 per 2 è dispari)
-------------------------------------------
i⁴⁷=-i
perché 47 è dispari,
i⁴⁷ = -i (il quoziente 23 della divisione di 47 per 2 è dispari)
-------------------------------------------
i²¹=i
perché 21 è dispari,
i²¹ = i (il quoziente 10 della divisione di 21 per 2 è pari)
-------------------------------------------
i⁴¹=i
perché 41 è dispari,
i⁴¹ = i (il quoziente 20 della divisione di 41 per 2 è pari)
-------------------------------------------
Dopo aver calcolato le potenze presenti nella prima espressione dell' esercizio n. 1, facciamo le sostituzioni e calcoliamo:
[-i-5(-i)+4(-i)]:(2i+3i)=
= [-i+5i-4i]:5i =
= 0:5i = 0 ☺️
Se questo approccio ti sembra un po' pesante, allora seguimi in questi semplici e pratici conticini:
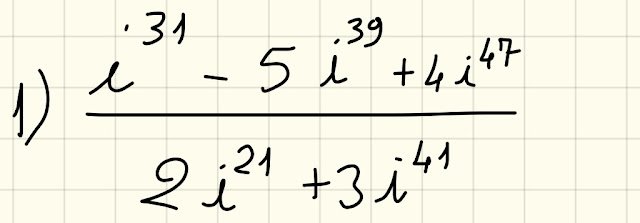 |
| Fig. 3 |
Guarda come scrivo gli esponenti delle potenze, sfruttando la divisione per 2, applicando, poi, le proprietà delle potenze:
 |
| Fig. 4 Potenze al numeratore |
Anche qui sotto faccio la stessa cosa:
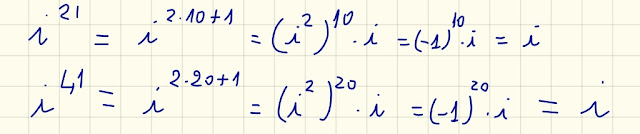 |
| Fig. 5 Potenze al denominatore |
Una volta calcolate le potenze di i, calcolo l' espressione assegnata:
 |
| Fig. 6 |
Passiamo adesso alla seconda espressione, e la calcoliamo facendo i conticini semplici e pratici:
 |
| Fig. 7 |
Sfrutto la divisione dell' esponente per 2, applico le proprietà delle potenze e il gioco è fatto! ☺️
 |
| Fig. 8 |
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
👇👇👇
Guarda questo tutorial in video:
Tags, etichette:
esercizi svolti numeri complessi,
numeri complessi,
potenza di un numero complesso,
potenza unità immaginaria,
potenze di i
Numeri Complessi: Esercizi Svolti
Ultimo Aggiornamento: 10/04/2020
A queste e ad altre domande risponderemo con lo svolgimento di alcuni esercizi.
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 3 esercizi.
Esercizio 1
Trovare i valori reali di x e y affinché i numeri complessi
z=3x+1+(x-y+2)i
e
w=x-y+2xi
siano uguali.
Svolgo
Due numeri complessi sono uguali se e solo se hanno parti reali uguali e coefficienti delle parti immaginarie anch' essi uguali.
z=a+bi, w=c+di
z=w ⇔ a=c ed anche b=d
Dunque dobbiamo (im)porre
3x+1=x-y
ed anche
x-y+2=2x
Ecco, queste due ultime equazioni che abbiamo scritto devono essere soddisfatte entrambe, quindi insieme costituiscono un sistema di due equazioni e due incognite, x ed y.
Risolviamolo col semplice metodo di sostituzione:
I valori reali di x e y per i quali i numeri complessi assegnati, z e w, sono uguali sono
x=-3 e y=5,
infatti, sostituendo, si ha:
z=3x+1+(x-y+2)i
z=3(-3)+1+(-3-5+2)i
z=-8+(-6)i
e
w=x-y+2xi
w=-3-5+2(-3)i
w=-8+(-6)i
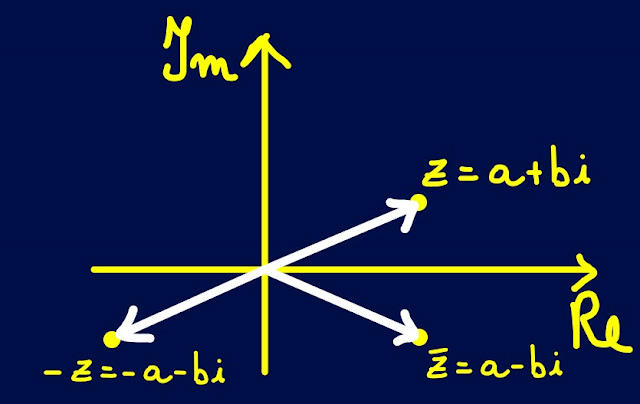
Entrambi i numeri complessi, z e w, sono rappresentati dallo stesso punto sul piano di Gauss (o piano complesso):
z=(-8, -6) e w=(-8, -6)
Esercizio 2
Trovare il valore reale di h per il quale il modulo del numero complesso
z=1+2h+(h-1)i
sia uguale a 3
Svolgo
0⋅x=2 è impossibile!
Non c'è alcun valore reale di x che moltiplicato per zero dia come risultato 2.
Pertanto non ci sono valori reali per x ed y che rendano i due numeri complessi l' uno l' opposto dell' altro.
Passiamo al punto 2)
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Che cos' è il modulo di un numero complesso?
Che cosa si intende per coniugato di un numero complesso?
A queste e ad altre domande risponderemo con lo svolgimento di alcuni esercizi.
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 3 esercizi.
Esercizio 1
Trovare i valori reali di x e y affinché i numeri complessi
z=3x+1+(x-y+2)i
e
w=x-y+2xi
siano uguali.
Svolgo
Numeri complessi uguali (condizione):
Due numeri complessi sono uguali se e solo se hanno parti reali uguali e coefficienti delle parti immaginarie anch' essi uguali.
z=a+bi, w=c+di
z=w ⇔ a=c ed anche b=d
Dunque dobbiamo (im)porre
3x+1=x-y
ed anche
x-y+2=2x
Ecco, queste due ultime equazioni che abbiamo scritto devono essere soddisfatte entrambe, quindi insieme costituiscono un sistema di due equazioni e due incognite, x ed y.
Risolviamolo col semplice metodo di sostituzione:
I valori reali di x e y per i quali i numeri complessi assegnati, z e w, sono uguali sono
x=-3 e y=5,
infatti, sostituendo, si ha:
z=3x+1+(x-y+2)i
z=3(-3)+1+(-3-5+2)i
z=-8+(-6)i
e
w=x-y+2xi
w=-3-5+2(-3)i
w=-8+(-6)i
Entrambi i numeri complessi, z e w, sono rappresentati dallo stesso punto sul piano di Gauss (o piano complesso):
z=(-8, -6) e w=(-8, -6)
Esercizio 2
Trovare il valore reale di h per il quale il modulo del numero complesso
z=1+2h+(h-1)i
sia uguale a 3
Svolgo
Modulo di un numero complesso: come si calcola
Sappiamo che il modulo di un numero complesso
z=a+bi,
che si indica con la scrittura |a+bi|,
è dato dalla radice quadrata della somma tra il quadrato della parte reale e il quadrato del coefficiente della parte immaginaria:
|a+bi|=√(a²+b²)
Applichiamo dunque questa formula del modulo di un numero complesso qualsiasi al nostro numero complesso particolare:
|z|=|1+2h+(h-1)i|=
=√(a²+b²)=
=√[(1+2h)²+(h-1)²]
Poiché |z|=3,
scriviamo
√[(1+2h)²+(h-1)²]=3
Questa che cos' è?
E' un' equazione nell' incognita h, che risolviamo.
Eleviamo al quadrato 1° e 2° membro:
(1+2h)²+(h-1)²=9
Sviluppiamo i quadrati dei binomi:
1+4h²+4h+h²+1-2h=9
Scriviamo questa equazione di secondo grado nella sua forma canonica:
5h²+2h-7=0
Calcoliamo il discriminante (Δ/4):
Δ/4 = 1-5(-7) = 36
Formula risolutiva:
h₁₂=(-1±6)/5 ⇾
h₁=-7/5
oppure
h₂=1
Infatti, sostituendo i valori di h trovati, otteniamo due numeri complessi che hanno lo stesso modulo, 3.
Essi sono:
per h₁=-7/5
z₁=1+2(-7/5)+[(-7/5)-1]i=
= -9/5-(12/5)i
per h₂=1
z₂=1+2⋅1+(1-1)i =
= 3+0⋅i= 3
Esercizio 3
Siano z e w due numeri complessi:
z=x+2-yi
w=x-y+2xi
Trova i valori reali di x e y affinché z e w siano:
1) opposti;
2) coniugati.
Svolgo
Numeri complessi opposti
Numeri complessi coniugati
1) z e w sono opposti se z=-w, dunque
x+2-yi=-[x-y+2xi]
x+2-yi=-x+y-2xi
Adesso imponiamo l' uguaglianza tra le due parti reali l' uguaglianza tra i due coefficienti delle parti immaginarie:
x+2=-x+y
ed anche
-y=-2x
Queste due ultime equazioni insieme costituiscono un sistema di due equazioni e due incognite, x ed y, che risolviamo:
0⋅x=2 è impossibile!
Non c'è alcun valore reale di x che moltiplicato per zero dia come risultato 2.
Pertanto non ci sono valori reali per x ed y che rendano i due numeri complessi l' uno l' opposto dell' altro.
Passiamo al punto 2)
z=x+2-yi
w=x-y+2xi
Affinché z e w siano coniugati dobbiamo imporre che
x+2=x-y
(cioè parti reali uguali)
ed anche
-y = - 2x
(cioè coefficiente della parte immaginaria dell' uno uguale all' opposto del coefficiente della parte immaginaria dell' altro)
Di nuovo, queste due ultime equazioni insieme costituiscono un sistema di due equazioni e due incognite, x ed y, che risolviamo:
Infatti, per questi due valori di x ed y, si ha che
Affinché z e w siano coniugati dobbiamo imporre che
x+2=x-y
(cioè parti reali uguali)
ed anche
-y = - 2x
(cioè coefficiente della parte immaginaria dell' uno uguale all' opposto del coefficiente della parte immaginaria dell' altro)
Di nuovo, queste due ultime equazioni insieme costituiscono un sistema di due equazioni e due incognite, x ed y, che risolviamo:
Infatti, per questi due valori di x ed y, si ha che
z=x+2-yi
z=-1+2-(-2)i
z=1+2i
e
z=-1+2-(-2)i
z=1+2i
e
w=x-y+2xi
w=-1-(-2)+2(-1)i
w=1-2i
z e w sono coniugati ☺️
w=-1-(-2)+2(-1)i
w=1-2i
z e w sono coniugati ☺️
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
👇👇👇
Guarda questa esercitazione in video:
Numeri Complessi: Proprietà Commutativa dell' Addizione e della Moltiplicazione
Ultimo Aggiornamento: 09/04/2020
Nell' insieme dei numeri complessi vale la proprietà commutativa dell' addizione e della moltiplicazione?
z + w = w + z ∀ z,w ∈ C ?
z ⋅ w = w ⋅ z ∀ z,w ∈ C ?
∀ z,w ∈ C si legge "per ogni (∀) coppia di elementi, z e w, appartenenti (∈) all' insieme dei Numeri Complessi (C)"
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
Per gli amanti delle dimostrazioni matematiche, in questo breve tutorial, risponderò ai due quesiti precedenti.
Esercizio
Dimostra che la moltiplicazione e l' addizione nell' insieme dei numeri complessi ( C ) godono della proprietà commutativa.
Svolgimento
Prendiamo due numeri complessi qualunque, scritti in forma algebrica:
z = a + i⋅b
w = c + i⋅d
a, b, c, d sono numeri reali
a e c sono le parti reali rispettivamente di z e w;
b e d sono i coefficienti delle parti immaginarie rispettivamente di z e w
i è l' unità immaginaria, il cui quadrato fa -1:
i² = -1
z + w = (a + i⋅b) + (c + i⋅d) =
...per definizione di somma di due numeri complessi...
= (a+c)+i⋅(b+d)
Cos' è successo?
E' successo che la parte reale è la somma delle parti reali, e il coefficiente della parte immaginaria è la somma dei coefficienti delle parti immaginarie.
Per la proprietà commutativa dell' addizione nei numeri reali...
z + w = (a+c)+i⋅(b+d) =
= (c+a)+i⋅(d+b) =
...per la definizione di somma di due numeri complessi vista prima...
= (c + i⋅d) + (a + i⋅b) =
= w + z
Ricordiamolo:
la parte reale è la somma delle parti reali; il coefficiente della parte immaginaria è la somma dei coefficienti delle parti immaginarie.
Guardando la catena di uguaglianze, possiamo concludere che
z + w = w + z ∀ z,w ∈ C ! ☺️
Andiamo avanti con la moltiplicazione...
z⋅w = (a + i⋅b) ⋅ (c + i⋅d) =
...per definizione di prodotto di due numeri complessi...
= (a⋅c-b⋅d)+i⋅(a⋅d+b⋅c)
Osserviamo quello che è successo:
la parte reale è la differenza tra il prodotto delle parti reali e il prodotto dei coefficienti delle parti immaginarie;
il coefficiente della parte immaginaria invece è la somma tra il prodotto dei due coefficienti "estremi" (diciamo così, per semplicità) e il prodotto dei due "medi" (anche qui diciamo così, per semplicità).
Andiamo avanti...
(a⋅c-b⋅d)+i⋅(a⋅d+b⋅c)=
...per la proprietà commutativa della moltiplicazione nei numeri reali...
= (c⋅a-d⋅b)+i⋅(d⋅a+c⋅b) =
...per la proprietà commutativa dell' addizione nei numeri reali...
= (c⋅a-d⋅b)+i⋅(c⋅b+d⋅a) =
...per la definizione di prodotto di due numeri complessi vista prima...
= (c + i⋅d) ⋅ (a + i⋅b) = w⋅z
Ricordiamolo:
la parte reale è la differenza tra il prodotto delle parti reali e il prodotto dei coefficienti delle parti immaginarie;
il coefficiente della parte immaginaria invece è la somma tra il prodotto dei due coefficienti "estremi" e il prodotto dei due "medi".
Guardando la catena di uguaglianze, possiamo concludere che
z ⋅ w = w ⋅ z ∀ z,w ∈ C ! ☺️
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Guarda questa esercitazione in video:
 |
| Fig. 1 |
Nell' insieme dei numeri complessi vale la proprietà commutativa dell' addizione e della moltiplicazione?
z + w = w + z ∀ z,w ∈ C ?
z ⋅ w = w ⋅ z ∀ z,w ∈ C ?
∀ z,w ∈ C si legge "per ogni (∀) coppia di elementi, z e w, appartenenti (∈) all' insieme dei Numeri Complessi (C)"
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
Per gli amanti delle dimostrazioni matematiche, in questo breve tutorial, risponderò ai due quesiti precedenti.
Esercizio
Dimostra che la moltiplicazione e l' addizione nell' insieme dei numeri complessi ( C ) godono della proprietà commutativa.
Svolgimento
Prendiamo due numeri complessi qualunque, scritti in forma algebrica:
z = a + i⋅b
w = c + i⋅d
a, b, c, d sono numeri reali
a e c sono le parti reali rispettivamente di z e w;
b e d sono i coefficienti delle parti immaginarie rispettivamente di z e w
i è l' unità immaginaria, il cui quadrato fa -1:
i² = -1
z + w = (a + i⋅b) + (c + i⋅d) =
...per definizione di somma di due numeri complessi...
= (a+c)+i⋅(b+d)
Cos' è successo?
E' successo che la parte reale è la somma delle parti reali, e il coefficiente della parte immaginaria è la somma dei coefficienti delle parti immaginarie.
Per la proprietà commutativa dell' addizione nei numeri reali...
z + w = (a+c)+i⋅(b+d) =
= (c+a)+i⋅(d+b) =
...per la definizione di somma di due numeri complessi vista prima...
= (c + i⋅d) + (a + i⋅b) =
= w + z
Ricordiamolo:
la parte reale è la somma delle parti reali; il coefficiente della parte immaginaria è la somma dei coefficienti delle parti immaginarie.
Guardando la catena di uguaglianze, possiamo concludere che
z + w = w + z ∀ z,w ∈ C ! ☺️
Andiamo avanti con la moltiplicazione...
z⋅w = (a + i⋅b) ⋅ (c + i⋅d) =
...per definizione di prodotto di due numeri complessi...
= (a⋅c-b⋅d)+i⋅(a⋅d+b⋅c)
Osserviamo quello che è successo:
la parte reale è la differenza tra il prodotto delle parti reali e il prodotto dei coefficienti delle parti immaginarie;
il coefficiente della parte immaginaria invece è la somma tra il prodotto dei due coefficienti "estremi" (diciamo così, per semplicità) e il prodotto dei due "medi" (anche qui diciamo così, per semplicità).
Andiamo avanti...
(a⋅c-b⋅d)+i⋅(a⋅d+b⋅c)=
...per la proprietà commutativa della moltiplicazione nei numeri reali...
= (c⋅a-d⋅b)+i⋅(d⋅a+c⋅b) =
...per la proprietà commutativa dell' addizione nei numeri reali...
= (c⋅a-d⋅b)+i⋅(c⋅b+d⋅a) =
...per la definizione di prodotto di due numeri complessi vista prima...
= (c + i⋅d) ⋅ (a + i⋅b) = w⋅z
Ricordiamolo:
la parte reale è la differenza tra il prodotto delle parti reali e il prodotto dei coefficienti delle parti immaginarie;
il coefficiente della parte immaginaria invece è la somma tra il prodotto dei due coefficienti "estremi" e il prodotto dei due "medi".
Guardando la catena di uguaglianze, possiamo concludere che
z ⋅ w = w ⋅ z ∀ z,w ∈ C ! ☺️
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
👇👇👇
Guarda questa esercitazione in video:
Iscriviti a:
Post (Atom)
Ti potrebbero interessare anche questi post:
-
Ultimo aggiornamento: 28 11 2019 Questa esercitazione è consultabile gratuitamente online. Se vuoi anche scaricarla in formato P...
-
Ultimo aggiornamento: 02/01/2022 Che cos' è una funzione? Come si trova il dominio di una funzione? Come si classificano le funzioni? Ci...
-
ultimo aggiornamento: 04 12 2020 Grafici e Trasformazioni Geometriche Come si disegna il grafico di una funzione applicando le trasform...
-
In questa esercitazione, estratta dal mio Tutorial sulla Parabola , vedremo lo svolgimento di 2 esercizi di matematica per le Super...
-
Qui trovi le formule per calcolare: 1) il tempo di volo di un proiettile lanciato orizzontalmente ; 2) la gittata di un proiettile spara...
-
ISCRIVITI alla nostra Newsletter per ricevere gli aggiornamenti e i contenuti speciali pensati per gli iscritti. In questo post svolg...
-
In questo post, vedremo come si disegnano(senza utilizzare il computer❗️🤓🙄😀) delle funzioni, leggermente complesse, partendo dai grafic...
-
Ho preparato un video, lo trovi qui sotto, in cui svolgo e commento 4 equazioni goniometriche lineari in seno e coseno, sfruttando il meto...
-
In questa esercitazione sulle operazioni tra polinomi , che è la n° 3 su questo argomento, vedremo come si risolvono 4 esercizi. Dico su...
-
In questa esercitazione di matematica delle Superiori , che è divisa in 3 parti, vedremo come si determina il dominio di una funzione ...
Archivio blog
-
▼
2014
(291)
-
▼
febbraio
(43)
- SIMPATICHE TRASFORMAZIONI GEOMETRICHE
- PROBLEMA DI MINIMO, SVOLTO E COMMENTATO
- ESERCIZIO SVOLTO SUGLI ASINTOTI VERTICALI E ORIZZO...
- ESERCIZIO SVOLTO SUGLI ASINTOTI VERTICALI E ORIZZO...
- ESERCIZIO SUI MASSIMI, MINIMI E FLESSI, SFRUTTANDO...
- ESERCIZIO SVOLTO SUI MASSIMI E MINIMI ASSOLUTI
- ESERCIZIO RISOLTO SUI MASSIMI, MINIMI E FLESSI (ME...
- ESERCIZIO SUI PUNTI DI FLESSO (METODO DELLE DERIVA...
- ESERCIZIO SVOLTO SUI FLESSI (METODO DELLE DERIVATE...
- ESERCIZIO SVOLTO SUI MASSIMI, MINIMI E FLESSI COL ...
- ESERCIZIO SVOLTO SULLE EQUAZIONI DI II GRADO NELL'...
- ESERCIZIO SVOLTO SULLA FORMA ESPONENZIALE DEI NUME...
- ESERCIZIO SVOLTO SUI NUMERI COMPLESSI (OPERAZIONI)
- ESERCIZIO SVOLTO SUI NUMERI COMPLESSI: RADICE N-ES...
- ESERCIZIO RISOLTO SULLE OPERAZIONI TRA NUMERI COMP...
- ESERCIZIO SVOLTO SULLA RAPPRESENTAZIONE GONIOMETRI...
- ESERCIZIO SVOLTO SUI MASSIMI E MINIMI IN FUNZIONI ...
- ESERCIZIO SVOLTO SULLE EQUAZIONI (METODO GRAFICO)
- Calcolo Differenziale: come si applica il Teorema ...
- PROBLEMA SVOLTO COL DIFFERENZIALE DI UNA FUNZIONE
- ESERCIZIO SVOLTO SUL DIFFERENZIALE DI UNA FUNZIONE
- ESERCIZIO SVOLTO SUL DIFFERENZIALE DI UNA FUNZIONE
- STUDIARE MATEMATICA
- ESERCIZIO SVOLTO SUL TEOREMA DI CAUCHY
- ESERCIZIO SVOLTO SUL TEOREMA DI CAUCHY
- ESERCIZIO SVOLTO SUGLI INTEGRALI
- ESERCIZIO SVOLTO SUGLI INTEGRALI INDEFINITI
- Numeri Complessi: Potenze dell' Unità Immaginaria
- Numeri Complessi: Esercizi Svolti
- Numeri Complessi: Proprietà Commutativa dell' Addi...
- ESERCIZIO SVOLTO SUI LOGARITMI
- ESERCIZIO SVOLTO SULLE DERIVATE DELLE FUNZIONI CON...
- ESERCIZIO SVOLTO SUI TRIANGOLI
- ESERCIZIO SVOLTO SULLE FUNZIONI CONTINUE
- ESERCIZIO DI BASE SVOLTO SUI LOGARITMI
- ESERCIZIO DI BASE RISOLTO SUI LOGARITMI
- ESERCIZIO DI BASE RISOLTO SUI LOGARITMI
- ESERCIZIO DI BASE SVOLTO SUI LOGARITMI
- ESERCIZIO SVOLTO SUI LOGARITMI
- STUDIARE LA MATEMATICA
- ESERCIZIO SVOLTO: GRAFICO PROBABILE DI UNA FUNZIONE
- ESERCIZIO SVOLTO SUL CALCOLO COMBINATORIO: EQUAZIONE
- ESERCIZIO/PROBLEMA SVOLTO DI TRIGONOMETRIA APPLICA...
-
▼
febbraio
(43)