Numeri Complessi: Potenze dell' Unità Immaginaria

Ultimo Aggiornamento: 13/04/2020

Come si calcolano le potenze dell' unità immaginaria?

Quanto fa iⁿ, dove i è l' unità immaginaria ed n è un numero naturale?

Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.

Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.



In questo tutorial, ti propongo 2 espressioni che contengono potenze dell' unità immaginaria.

Esercizio 1

Calcola le seguenti espressioni:

Fig.1

In questo tutorial, ti voglio mostrare una tecnica di calcolo alternativa a quella proposta da alcuni manuali di matematica.

Anziché dividere l' esponente n per 4 (come probabilmente hai visto in classe o sul manuale di matematica), dividiamo per 2.

Vediamo perché:

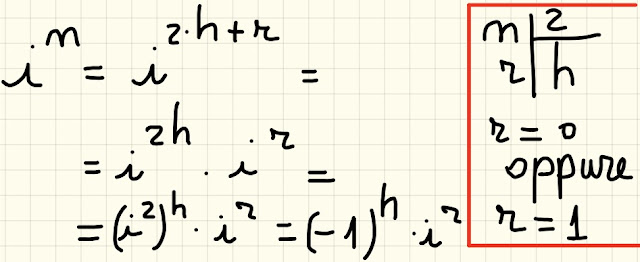Fig. 2

h è il quoziente della divisione dell' esponente n per 2 ed r è il resto, che può valere 0 (se n è pari) oppure 1 (se n è dispari).

Seguendo nella fig. 2 l' applicazione delle proprietà delle potenze, si arriva in fondo e si scopre che 

iⁿ = (-1)ᵸ ⋅ i⁰ =
   = (-1)ᵸ ⋅ 1 =
   = (-1)ᵸ      (se n è pari)

oppure

iⁿ = (-1)ᵸ ⋅ i¹ =
   = (-1)ᵸ ⋅ i      (se n è dispari)

Quindi 

se n è pari, 

iⁿ = -1 (se il quoziente h della divisione di n per 2 è dispari)

oppure 

iⁿ = 1 (se il quoziente h della divisione di n per 2 è pari)
-------------------------------------------

se n è dispari, 

iⁿ = -i (se il quoziente h della divisione di n per 2 è dispari)

oppure 

iⁿ = i (se il quoziente h della divisione di n per 2 è pari)

Potenze dell' unità immaginaria

Dopo aver fatto queste considerazioni sulla potenza iⁿ di carattere generale, affrontiamo le espressioni assegnate.

1)
Calcoliamo le singole potenze in gioco:

i³¹=-i

perché 31 è dispari, 

i³¹ = -i (il quoziente 15 della divisione di 31 per 2 è dispari)
-------------------------------------------

i³⁹=-i

perché 39 è dispari, 

i³⁹ = -i (il quoziente 19 della divisione di 39 per 2 è dispari)
-------------------------------------------

i⁴⁷=-i

perché 47 è dispari, 

i⁴⁷ = -i (il quoziente 23 della divisione di 47 per 2 è dispari)
-------------------------------------------

i²¹=i

perché 21 è dispari, 

i²¹ = i (il quoziente 10 della divisione di 21 per 2 è pari)
-------------------------------------------

i⁴¹=i

perché 41 è dispari, 

i⁴¹ = i (il quoziente 20 della divisione di 41 per 2 è pari)
-------------------------------------------

Dopo aver calcolato le potenze presenti nella prima espressione dell' esercizio n. 1, facciamo le sostituzioni e calcoliamo:

[-i-5(-i)+4(-i)]:(2i+3i)=

= [-i+5i-4i]:5i =

= 0:5i = 0   ☺️

Se questo approccio ti sembra un po' pesante, allora seguimi in questi semplici e pratici conticini:

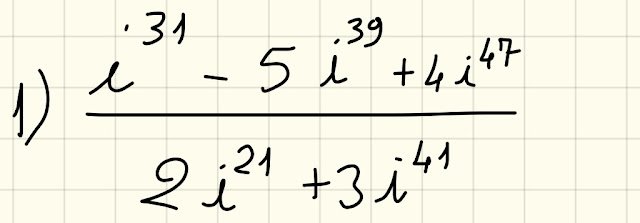Fig. 3

Guarda come scrivo gli esponenti delle potenze, sfruttando la divisione per 2, applicando, poi, le proprietà delle potenze:

Fig. 4

Potenze al numeratore

Anche qui sotto faccio la stessa cosa:

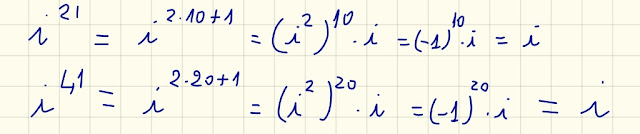Fig. 5

Potenze al denominatore

Una volta calcolate le potenze di i, calcolo l' espressione assegnata:

Fig. 6

Passiamo adesso alla seconda espressione, e la calcoliamo facendo i conticini semplici e pratici:

Fig. 7

Sfrutto la divisione dell' esponente per 2, applico le proprietà delle potenze e il gioco è fatto! ☺️

Fig. 8

Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto: 

troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore. 

Alla prossima lezione. Ciao, ti aspetto!

👇👇👇

Impara di più >

Guarda questo tutorial in video: