In questa esercitazione, vedremo
Esercizio
come si applica il Teorema di Rolle.
Si dimostri che il grafico della funzione
y=f(x)=x⁵+x³+1
interseca l' asse delle ascisse in un solo punto.
Faremo una
dimostrazione per assurdo.
esercizi svolti di matematica
per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
La funzione assegnata è polinomiale, quindi è continua e derivabile su tutto ℝ (l' insieme dei numeri reali).
Ora calcoliamo i seguenti limiti:
lim x⁵+x³+1 = -∞
x➝-∞
e
lim x⁵+x³+1 = +∞
x➝+∞
x➝+∞
I valori di questi due limiti ci autorizzano ad affermare che il grafico della funzione interseca almeno una volta l' asse delle ascisse, dato che la funzione è continua.
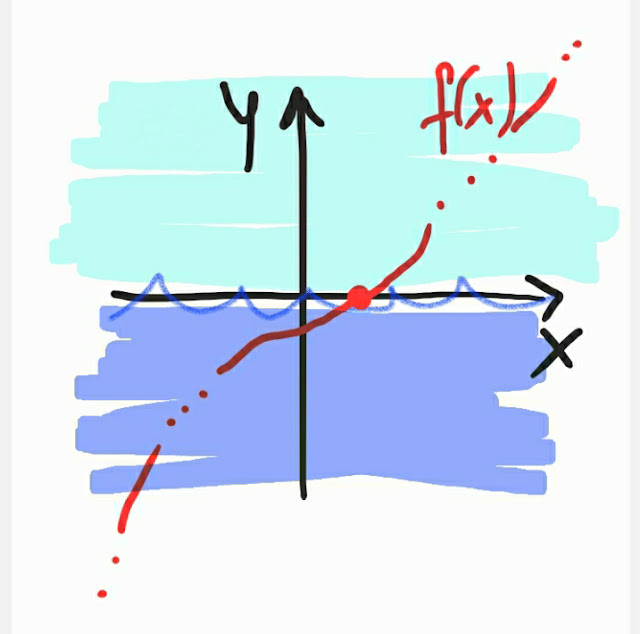
Cerco di spiegarlo meglio utilizzando l' immagine "mare-cielo" qui sotto della fig. 1:
Quando x tende a -∞ la funzione tende a
-∞ (cioè il suo grafico si trova nelle "profondità del mare"); mentre quando x tende a +∞ la funzione tende a +∞ (cioè il suo grafico si trova "alto nel cielo").
Dunque, da qualche parte, il grafico continuo della funzione interseca "la superficie del mare" (punto di incrocio tra il grafico della funzione e l' asse x).
Bene, torniamo all' esercizio!
Dunque c = 0
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
Prima di andare avanti, ci tengo a dirti che puoi imparare di più attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è
Matematica Quinquennio
Se vuoi scoprire di più e iniziare un percorso, fai click sul link qui sotto:
Bene, torniamo all' esercizio!
Ammettiamo che ci siano due punti distinti,
x₁ e x₂, tali che
f(x₁)=f(x₂)=0
Ammettiamo cioè che ci siano due punti distinti in cui il grafico della funzione interseca l' asse x.
Osserviamo che questa ammissione porta ad una prima conseguenza:
1) sono soddisfatte le ipotesi del
teorema di Rolle
sull' intervallo [x₁, x₂] per la funzione
f(x)=x⁵+x³+1
Allora esiste (∃) un valore c appartenente (∊) all' intervallo
]x₁, x₂[
tale che
f '(c) = 0,
cioè esiste una soluzione, c, per l' equazione
5x⁴+3x²=0
Infatti, essendo
f(x)=x⁵+x³+1 ,
si ha che
f '(x) = 5x⁴+3x² ,
e l' equazione da risolvere è
f '(c) = 5c⁴+3c² = 0 (c incognita).
Cerchiamo questo valore c (userò la lettera x che mi piace di più per indicare un' incognita):
5x⁴+3x² = 0
Raccolgo il fattor comune x² :
x²(5x²+3)=0
segue che
x²=0 ➝ x=0
oppure
5x²+3=0 ➝ x²=-3/5 (impossibile)
Dunque c = 0
Poiché c = 0 è interno all' intervallo
[x₁, x₂]
si ha che
x₁<0 e x₂>0 (x₁ e x₂ sono discordi)
Ricordiamoci di questa prima conseguenza!
Ammettere che ci sono due punti distinti,
x₁ ≠ x₂, tali che
f(x₁)=f(x₂)=0
porta ad una seconda conseguenza:
2)
f(x₁)=x₁⁵+x₁³+1=0
↓
x₁⁵+x₁³=-1
↓
x₁³(x₁²+1)=-1
↓
x₁<0
Perché x₁<0 ?
Beh, dato che (x₁²+1)>0 e il prodotto fa -1 (negativo), necessariamente deve essere
x₁³<0, e quindi x₁<0
Teniamo in memoria il fatto che
x₁<0
Non abbiamo finito!
Analogo ragionamento su
f(x₂) :
f(x₂)=x₂⁵+x₂³+1=0
↓
x₂⁵+x₂³=-1
↓
x₂³(x₂²+1)=-1
↓
x₂<0
Perché x₂<0 ?
Beh, per lo stesso motivo visto prima:
dato che (x₂²+1)>0 e il prodotto fa -1 (negativo), necessariamente deve essere
x₂³<0, e quindi x₂<0
Come vedi, l' avere ammesso che ci sono due punti distinti,
x₁ ≠ x₂, tali che
f(x₁)=f(x₂)=0
ci ha portato a due conseguenze contraddittorie tra di loro:
1) x₁<0 e x₂>0 (x₁ e x₂ sono discordi);
😲
2) x₁<0 e x₂<0 (x₁ e x₂ sono concordi, entrambi negativi)
Ecco, siccome ammettere l' esistenza di due punti distinti,
x₁ ≠ x₂, tali che
f(x₁)=f(x₂)=0 porta ad una contraddizione, possiamo concludere che NON esistono due punti distinti in cui il grafico della funzione interseca l' asse delle ascisse.
Ne esisite solo uno!
Perché?
Perché i valori dei due limiti che abbiamo calcolato all' inizio ci autorizzano ad affermare che il grafico della funzione interseca almeno una volta l' asse delle ascisse.
Siccome due punti di intersezione distinti non sono ammessi, possiamo concludere che il grafico della funzione interseca l' asse delle ascisse in un solo punto.
Abbiamo visto un esempio di
come si fa una dimostrazione per assurdo.
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!












Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)