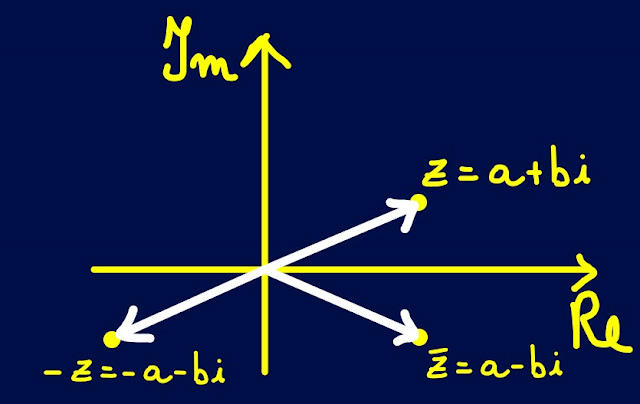
Che cos' è il modulo di un numero complesso?
Che cosa si intende per coniugato di un numero complesso?
A queste e ad altre domande risponderemo con lo svolgimento di alcuni esercizi.
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 3 esercizi.
Esercizio 1
Trovare i valori reali di x e y affinché i numeri complessi
z=3x+1+(x-y+2)i
e
w=x-y+2xi
siano uguali.
Svolgo
Numeri complessi uguali (condizione):
Due numeri complessi sono uguali se e solo se hanno parti reali uguali e coefficienti delle parti immaginarie anch' essi uguali.
z=a+bi, w=c+di
z=w ⇔ a=c ed anche b=d
Dunque dobbiamo (im)porre
3x+1=x-y
ed anche
x-y+2=2x
Ecco, queste due ultime equazioni che abbiamo scritto devono essere soddisfatte entrambe, quindi insieme costituiscono un sistema di due equazioni e due incognite, x ed y.
Risolviamolo col semplice metodo di sostituzione:
I valori reali di x e y per i quali i numeri complessi assegnati, z e w, sono uguali sono
x=-3 e y=5,
infatti, sostituendo, si ha:
z=3x+1+(x-y+2)i
z=3(-3)+1+(-3-5+2)i
z=-8+(-6)i
e
w=x-y+2xi
w=-3-5+2(-3)i
w=-8+(-6)i
Entrambi i numeri complessi, z e w, sono rappresentati dallo stesso punto sul piano di Gauss (o piano complesso):
z=(-8, -6) e w=(-8, -6)
Esercizio 2
Trovare il valore reale di h per il quale il modulo del numero complesso
z=1+2h+(h-1)i
sia uguale a 3
Svolgo
Modulo di un numero complesso: come si calcola
Sappiamo che il modulo di un numero complesso
z=a+bi,
che si indica con la scrittura |a+bi|,
è dato dalla radice quadrata della somma tra il quadrato della parte reale e il quadrato del coefficiente della parte immaginaria:
|a+bi|=√(a²+b²)
Applichiamo dunque questa formula del modulo di un numero complesso qualsiasi al nostro numero complesso particolare:
|z|=|1+2h+(h-1)i|=
=√(a²+b²)=
=√[(1+2h)²+(h-1)²]
Poiché |z|=3,
scriviamo
√[(1+2h)²+(h-1)²]=3
Questa che cos' è?
E' un' equazione nell' incognita h, che risolviamo.
Eleviamo al quadrato 1° e 2° membro:
(1+2h)²+(h-1)²=9
Sviluppiamo i quadrati dei binomi:
1+4h²+4h+h²+1-2h=9
Scriviamo questa equazione di secondo grado nella sua forma canonica:
5h²+2h-7=0
Calcoliamo il discriminante (Δ/4):
Δ/4 = 1-5(-7) = 36
Formula risolutiva:
h₁₂=(-1±6)/5 ⇾
h₁=-7/5
oppure
h₂=1
Infatti, sostituendo i valori di h trovati, otteniamo due numeri complessi che hanno lo stesso modulo, 3.
Essi sono:
per h₁=-7/5
z₁=1+2(-7/5)+[(-7/5)-1]i=
= -9/5-(12/5)i
per h₂=1
z₂=1+2⋅1+(1-1)i =
= 3+0⋅i= 3
Esercizio 3
Siano z e w due numeri complessi:
z=x+2-yi
w=x-y+2xi
Trova i valori reali di x e y affinché z e w siano:
1) opposti;
2) coniugati.
Svolgo
Numeri complessi opposti
Numeri complessi coniugati
1) z e w sono opposti se z=-w, dunque
x+2-yi=-[x-y+2xi]
x+2-yi=-x+y-2xi
Adesso imponiamo l' uguaglianza tra le due parti reali l' uguaglianza tra i due coefficienti delle parti immaginarie:
x+2=-x+y
ed anche
-y=-2x
Queste due ultime equazioni insieme costituiscono un sistema di due equazioni e due incognite, x ed y, che risolviamo:
0⋅x=2 è impossibile!
Non c'è alcun valore reale di x che moltiplicato per zero dia come risultato 2.
Pertanto non ci sono valori reali per x ed y che rendano i due numeri complessi l' uno l' opposto dell' altro.
Passiamo al punto 2)
z=x+2-yi
w=x-y+2xi
Affinché z e w siano coniugati dobbiamo imporre che
x+2=x-y
(cioè parti reali uguali)
ed anche
-y = - 2x
(cioè coefficiente della parte immaginaria dell' uno uguale all' opposto del coefficiente della parte immaginaria dell' altro)
Di nuovo, queste due ultime equazioni insieme costituiscono un sistema di due equazioni e due incognite, x ed y, che risolviamo:
Infatti, per questi due valori di x ed y, si ha che
Affinché z e w siano coniugati dobbiamo imporre che
x+2=x-y
(cioè parti reali uguali)
ed anche
-y = - 2x
(cioè coefficiente della parte immaginaria dell' uno uguale all' opposto del coefficiente della parte immaginaria dell' altro)
Di nuovo, queste due ultime equazioni insieme costituiscono un sistema di due equazioni e due incognite, x ed y, che risolviamo:
Infatti, per questi due valori di x ed y, si ha che
z=x+2-yi
z=-1+2-(-2)i
z=1+2i
e
z=-1+2-(-2)i
z=1+2i
e
w=x-y+2xi
w=-1-(-2)+2(-1)i
w=1-2i
z e w sono coniugati ☺️
w=-1-(-2)+2(-1)i
w=1-2i
z e w sono coniugati ☺️
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
👇👇👇
Guarda questa esercitazione in video:



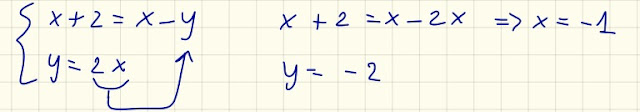










Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)