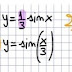In questa esercitazione di matematica delle Superiori, che è divisa in 3 parti, vedremo come si determina il dominio di una funzione.
Analizzeremo le tipologie delle funzioni più comuni.
Nella prima parte, le funzioni di cui vogliamo determinare i domini sono queste:
In questo primo blocco, determineremo quindi il dominio di una funzione polinomiale, il dominio di una funzione razionale fratta, il dominio di funzioni irrazionali.
 |
| Per iscriverti GRATIS fai click qui |
Nella 2ª parte, determineremo i domini di alcune funzioni logaritmiche ed esponenziali.
In particolare, vedremo come si trova il dominio di una funzione avente un numero IRRAZIONALE come esponente.
Nella 3ª parte, determineremo i domini di alcune funzioni goniometriche e vedremo anche come trovare il dominio di una funzione che ha un' altra funzione come esponente.
Cominciamo dalla prima: si tratta di una funzione polinomiale.
Tutte le funzioni del tipo y = f(x), dove f(x) è un polinomio, hanno per dominio tutto R, l' insieme dei numeri reali.
La funzione polinomiale ha senso per TUTTI i valori reali, cioè la variabile x può assumere qualunque valore. Possiamo attribuire alla x di una funzione polinomiale qualsiasi numero. Non esiste nemmeno un valore reale che faccia perdere significato alla funzione.
Ti ricordo che una funzione polinomiale nella variabile x è un' espressione di questo tipo:
Dove le x hanno esponenti che sono numeri naturali, che ho evidenziato in viola, e i coefficienti "a", che ho evidenziato in giallo, sono numeri reali.
Ora, osservate le seguenti funzioni:
La prima, quella con un solo asterisco, è una funzione polinomiale, dunque il suo dominio è tutto R, l' insieme dei numeri reali; mentre la seconda funzione, quella con due stelline, NON è polinomiale!!
Perchè??
Fammi sapere nei commenti! ✏️
Prima di passare al 2º esercizio, ti invito a iscriverti al mio canale Youtube per non perdere i nuovi video che arriveranno.
Utilizza i link che ho inserito, affinchè tu abbia accesso a tutte le altre risorse che metto a tua disposizione.
Andiamo avanti con la prossima funzione:
Questa funzione presenta una linea di frazione, che indica l' operazione di divisione.
Sappiamo che non si può dividere per zero.
Dunque dobbiamo imporre che il denominatore, cioè l' espressione che compare sotto la linea di frazione, sia diverso da zero.
Il dominio è fatto di tutti i valori reali tranne quelli che eventualmente annullano il denominatore.
In pratica, quindi, si pone uguale a zero il denominatore...
...e si risolve l' equazione che proviene appunto dal porre uguale a zero il denominatore.
Una volta risolta questa equazione, dovremo escludere le sue soluzioni, cioè le sue radici, perchè sono i valori che azzerano, rendono nullo, il denominatore.
Risolviamo l' equazione, facendo delle opportune manipolazioni.
Abbiamo scomposto il denominatore come prodotto di polinomi irriducibili.
Questo prodotto è nullo quando il primo fattore (x-1) vale zero oppure quando il secondo fattore (x+1) vale zero oppure quando il terzo fattore (2x-1) si annulla.
Questi tre valori azzerano il denominatore, dunque dobbiamo escluderli.
Scriviamo che il dominio è...
Un modo alternativo di scrivere il dominio è questo:
Ciò significa che togliamo dall' insieme R un suo sottoinsieme costituito dagli elementi -1, 1/2, 1, che azzerano il denominatore.
C' è un altro modo per rappresentare questo dominio. Lo sai?
Scrivilo nei commenti!✏️
Nella sezione dedicata ai commenti puoi anche porre domande, chiedere chiarimenti o altro.
Non si accettano commenti anonimi.😀
Vi do un suggerimento, visualizzando il dominio di questa funzione mediante un disegno:
Tutta la retta dei numeri reali, disegnata in verde, "bucata" in corrispondenza dei valori che annullano il denominatore, rappresenta il dominio.
Abbiamo quattro intervalli che compongono il dominio.
Quali sono questi quattro intervalli?
In quale altro modo possiamo scrivere il dominio?
Prossima funzione:
Prima di determinare il dominio di questa 3ª funzione, considera la possibilità di sostenere questo blog con un aiuto concreto...💝👇💝👇
💛 Fai clic sul Pulsante Donazione e aiutaci a realizzare nuove lezioni GRATUITE 💛 Grazie!!! 😊
Questa è una funzione del tipo...
Una funzione di questo tipo ha senso, per noi che in questo momento stiamo lavorando coi numeri reali, quando il radicando, f(x), è positivo o nullo.
Dobbiamo dunque imporre che
Risolviamo questa disequazione, partendo dalla sua equazione associata:
Calcoliamo il delta e applichiamo la formula risolutiva:
Disegniamo la parabola con la concavità verso l' alto, visto che il coefficiente che moltiplica x^2 è positivo, e prendiamo gli intervalli in cui il grafico della parabola sta sopra o interseca l' asse x.
Siccome la funzione che compare sotto la radice quadrata è positiva o nulla per x <= -3 oppure per x >= 2, il dominio è proprio
In quale altro modo si può scrivere questo dominio?
Scrivilo nei commenti!✏️
Nella sezione dedicata ai commenti puoi anche porre domande, chiedere chiarimenti o altro.
Non si accettano commenti anonimi.😀
Quarta funzione:
Una funzione di questo tipo ha senso quando il radicando, f(x), ha senso.
Poichè l' indice di radice, n, è dispari, il radicando, cioè la funzione f(x), può essere positivo, nullo o negativo. Dobbiamo escludere i valori della x per i quali la funzione non esiste.
Il valore della x per il quale la funzione evidenziata in rosa perde significato è 4, perchè per tale valore si annulla il denominatore, cioè si azzera 4-x.
La funzione che sta sotto la radice cubica può assumere qualunque valore: positivo, nullo o negativo; l' importante è escludere quei valori della x che fanno perdere significato alla funzione -1/(4-x).
Possiamo dunque scrivere che il dominio è...
Una funzione di questo tipo ha senso(esiste) per quei valori di x che rendono il radicando, f(x), positivo o nullo.
L' indice di radice è 2, che è pari.
Quindi imponiamo...
Risolviamo questa disequazione:
Qui trovi i miei eBooks, con ricchi esercizi svolti e commentati.
"Sciogliamo", per così dire, questa disequazione, togliendo il valore assoluto grazie all' applicazione della definizione di valore assoluto.
Un libro su cui puoi approfondire la teoria sui domini delle funzioni è il seguente:
Matematica Blu vol.5
Abbiamo moltiplicato per -1 i due membri della 1ª disequazione del 2º sistema(- x <= 3), e abbiamo cambiato il verso della disequazione di partenza(il <= è diventato >= perchė abbiamo moltiplicato 1º e 2º membro per un numero negativo, -1).
Visualizziamo le soluzioni.
Questa è la calcolatrice preferita dai miei studenti
Dove sono soddisfatte entrambe le disequazioncine di questo 1º sistema?
La risposta è...
A queste soluzioni dobbiamo unire quelle del secondo sistema.
Le due disequazioncine di questo 2º sistema sono soddisfatte entrambe per ...
Per i maturandi che affrontano la 2ª prova del liceo scientifico, è disponibile la
Calcolatrice Grafica senza calcolo simbolico, ammessa all' esame di maturità.
Unendo le soluzioni trovate, del 1º e 2º sistema, si ha che il dominio è dato da...
Il che vuol dire che
Se non lo hai ancora fatto, iscriviti al mio Canale Youtube:
Adesso è giunto il momento di affrontare le quattro funzioni della 2ª parte.
Eccole:
Nella 3ª parte, affronteremo anche alcune funzioni che provengono da un "pianeta" chiamato "goniometria"😄.
Partiamo dalla 1ª funzione di questo secondo blocco.
Diciamo subito che la x, poichè è argomento del logaritmo, deve essere strettamente maggiore di zero.
x > 0
Inoltre, dobbiamo imporre che il logaritmo, che compare sotto la linea di frazione, sia diverso da 2.
Perchè?
Perchè se il logaritmo assumesse il valore 2, avremmo sotto la linea di frazione uno zero, cioè 2-2, che è uguale a 0.
Siccome la linea di frazione sta ad indicare una divisione, non potendo dividere per zero, dobbiamo escludere anche quel valore della x che rende il logaritmo della nostra funzione uguale a 2.
Dobbiamo quindi chiederci per quale valore di x il logaritmo vale 2.
Dobbiamo risolvere questa equazioncina logaritmica che abbiamo appena scritto.
2 è l' esponente da dare alla base, 3, per avere l' argomento, x.
x è uguale a 3 al quadrato, cioè 9.
Dunque il dominio è dato da tutti i valori strettamente positivi, diversi da 9.
Come scriviamo questo dominio?
Seguimi sulla mia Pagina Facebook:
Lo scriviamo così:
D: x > 0, x ≠ 9
Se vogliamo visualizzare questo dominio, possiamo fare questo disegno:
La semiretta bucata in corrispondenza di x=9 e privata anche del punto in x=0 rappresenta il dominio.
In quale altro modo si può esprimere il dominio?
Scrivilo nei commenti✏️
Prima di passare al 2º esercizio, ti invito nuovamente ad iscriverti al mio canale Youtube(trovi il pulsante in questo post), per non perdere le mie nuove esercitazioni gratuite che arriveranno. Inoltre, segui i link che ho inserito, per accedere a tutte le altre risorse che ho messo a tua disposizione.
Seconda funzione:
Ti ricordo che una funzione del tipo
esiste per quei valori di x in cui esiste l' esponente f(x).
La nostra 2ª funzione assegnata è data dalla somma di tre funzioni di questo tipo. Vediamo:
Ecco, 5, 2 e 3 sono numeri positivi e diversi da 1.
Poi, gli esponenti x ed anche -(1-2x) non creano problemi perchè esistono per ogni valore reale della x.
L' unico esponente che fa suonare la sirena🚨 è l' esponente di 5, cioè 1/x.
Esso ha senso per x diverso da zero. Perchè??
Beh, perchè non ha senso dividere 1 per zero.
Dunque la nostra seconda funzione assegnata ha senso(esiste) per i valori di x diversi da zero.
Il dominio è
Terza funzione:
Questa 3ª funzione può essere vista in questo modo:
Tra un pò dirò alcune cose generali circa la funzione potenza con base ed esponente variabili, come la funzione che stiamo trattando.
La funzione che abbiamo appena scritto è assolutamente equivalente alla funzione assegnata. Se non ti è chiaro, prova a ricordare la definizione di logaritmo.
In questo caso, il logaritmo naturale di "qualcosa" è l' esponente da dare al numero "e"(la costante di Nepero) per ottenere quel "qualcosa".
Quel "qualcosa" non è altro che l' argomento del logaritmo.
Ora, applicando una proprietà dei logaritmi, si ha che
La radice quadrata di 2 meno x, che prima era esponente dell' argomento del logaritmo, è "sceso giù" ed è andato a moltiplicare il logaritmo.
Adesso, avendo riscritto la nostra 3ª funzione in questo modo, cioè coinvolgendo il numero di Nepero e il logaritmo naturale, ci accorgiamo che questa funzione ha senso quando l' argomento del logaritmo è strettamente maggiore di zero. Perchè ci preoccupiamo dell' argomento del logaritmo naturale? Perchè esso deve essere strettamente maggiore di zero, mentre l' esponente evidenziato in giallo esiste per qualunque valore reale della x.
Dunque imponiamo che
Tra un pò risolveremo questa disequazione, ma prima permettetemi di dire alcune cose generali.
In pratica, quando abbiamo a che fare con una funzione del tipo
ricordiamoci che essa viene vista come
Per tale motivo, la base f(x) va posta strettamente maggiore di zero, in quanto è intrappolata come argomento del logaritmo, e bisogna anche tener conto dei valori della variabile x per i quali ha senso la funzione g(x) evidenziata in giallo.
Bene, tornando alla nostra funzione, risolviamo la disequazione che abbiamo ottenuto prima, per poter determinare finalmente il nostro dominio.
Dato che il 2º fattore, sottolineato in verde, è positivo per qualunque valore della x, il prodotto che vediamo al 1º membro della disequazione è positivo quando il primo fattore, quello sottolineato in rosso, è positivo.
Esso è maggiore di zero per -1<x<1.
Il dominio è dunque
D: -1 < x < 1
Quarta e ultima funzione di questa 2ª parte:
👇👇👇
Instagram (clic), YouTube (clic), Linkedin (clic)
Facebook (clic), Google+ (clic), Twitter (clic)
Questo esercizio mi dà modo di fare un pò di chiarezza, perchè c' è un pò di confusione in giro per il mondo su questo tipo di funzione.
Quando abbiamo a che fare con una funzione potenza con base variabile, nel nostro esempio è x+1, ed esponente irrazionale, nel nostro esempio è radice quadrata di 2, essa può essere vista come funzione potenza a esponente REALE, che è definita imponendo la base variabile STRETTAMENTE maggiore di zero.
Questo perchè di nuovo possiamo riscrivere la nostra quarta funzione assegnata coinvolgendo il numero di Nepero(cioè la costante "e") e il logaritmo naturale, nel modo già visto prima:
Il dominio è pertanto l' insieme dei numeri reali più grandi di -1.
Bene!
Passiamo alla terza parte, in cui affronteremo queste altre quattro funzioni interessanti:
Tutto su Amazon:
La 1ª funzione di questa terza parte è
ed è del tipo
in cui sia la base, f(x), sia l' esponente, g(x), sono variabili.
Stando a quello che ho detto nella 2ª parte, che ti invito a guardare, dobbiamo imporre che la base sia strettamente maggiore di zero e dobbiamo tener conto anche dei valori della x per i quali esiste l' esponente.
L' esponente, cioè radice quadrata di x^2 - 1, esiste quando il radicando, cioè x^2 - 1, è maggiore o uguale a zero.
Tener conto anche dei valori di x per i quali l' esponente esiste, vuol dire risolvere questo sistema:
La 1ª disequazione del sistema nasce dal fatto che la base deve essere positiva e il radicando dell' esponente deve essere positivo o nullo.
Adesso ti mostro i passaggi per risolvere questo sistema:
Ti faccio notare che ho moltiplicato per -1 il 1º e il 2º membro della prima disequazione del sistema, ho cambiato i segni e il "maggiore" è diventato "minore".
Risolviamo le equazioni di 2º grado associate alle due disequazioni.
Ora calcoliamo il "delta" e applichiamo la formula risolutiva:
La 1ª disequazione è soddisfatta per
1/2 < x < 3.
Vediamo la 2ª equazione associata:
La 2ª disequazione è soddisfatta per
x <= -1 v x >= 1
Ora, con un grafico, vediamo dove sono soddisfatte entrambe le disequazioni:
C' è un solo intervallo in cui sono tutt' e due soddisfatte, quello in cui abbiamo due linee continue, cioè
Ecco, questo che abbiamo appena scritto rappresenta il dominio della funzione assegnata, perchè per questi valori della x la base è positiva e l' esponente esiste.
Prima di passare al 2º esercizio, ti invito ad iscriverti, per non perdere le mie nuove esercitazioni gratuite che arriveranno. Inoltre, segui i link che ho inserito, per accedere a tutte le altre risorse che ho messo a tua disposizione.
2ª funzione:
Per risolvere questa disequazione goniometrica, ricorriamo al disegno della circonferenza goniometrica:
Dalla figura si vede che gli angoli, senza tener conto degli omologhi, che vanno da -pigreco/2 a +pigreco/2 hanno il coseno positivo o nullo.
Dunque la seconda funzione assegnata esiste per, tenendo conto questa volta degli angoli omologhi,
Quello che abbiamo appena scritto è il dominio della seconda funzione assegnata.
Passiamo alla terza funzione:
Questa è una funzione del tipo
Dalla teoria sulle funzioni inverse delle funzioni goniometriche, sappiamo che l' argomento della funzione arco-coseno deve essere compreso tra -1 e 1, estremi inclusi.
Scriviamo dunque
Ciò significa
Scopriamo che i valori della x devono essere maggiori o uguali a -6 e minori o uguali a 6.
Il dominio della nostra terza funzione è
Quarta e ultima funzione di questa 3ª parte:
Guardando in faccia la funzione, ci rendiamo conto che essa ha senso quando:
• il radicando della radice quadrata è positivo o nullo;
• l' argomento del logaritmo naturale è strettamente maggiore di zero;
• il logaritmo, essendo sotto la linea di frazione, deve essere diverso da zero.
Scriviamo tutto questo.
Sappiamo che il logaritmo naturale si annulla quando il suo argomento, nel nostro caso x-1, vale 1.
In altre parole, non dobbiamo permettere che x-1 sia uguale a 1.
Scriviamolo:
Adesso, mettendo insieme le tre informazioni, si ha:
Visualizziamo...
Il dominio è fatto da tutti i valori strettamente maggiori di 2, perchè solo per tali valori sono soddisfatte tutt' e tre le condizioni.
Il dominio è dato da x > 2.
In una prossima esercitazione vedremo come si trovano i domini di funzioni più sostanziose.
Bene! Ti ricordo che puoi sostenere questo mio progetto didattico e consentirmi di realizzare altre esercitazioni gratuite, iscrivendoti, condividendo questo materiale didattico e, se vuoi, puoi anche fare una donazione. Donando puoi aiutarmi concretamente a dare continuità a questo servizio.
Grazie di cuore. A presto, ciao!