Sistemi lineari numerici fratti

Ultimo aggiornamento: 20 agosto 2019

In questa esercitazione, prima di affrontare un sistema di equazioni fratte, voglio farti vedere come si calcola il determinante di una matrice quadrata 2 x 2.

Esercizio 1

Calcola il determinante della matrice quadrata, 2 x 2, che vedi qui sotto nella Fig. 1.1

Fig. 1.1 determinante di una matrice 2 x 2

 Svolgimento Es. 1

Sui libri puoi trovare un altro modo di rappresentare il determinante di una matrice quadrata, come puoi vedere nella Fig. 2.1 qui sotto:

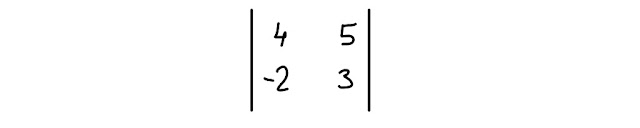Fig. 2.1 un altro modo per indicare il determinante di una matrice quadrata

 E' una notazione che ricorda il valore assoluto, ma in questo contesto specifico relativo alle matrici quadrate essa indica il determinante.

Ecco la regola:

Fig. 3.1 regola per calcolare il determinante di una matrice 2 x 2

 Come puoi vedere nella Fig. 3.1, abbiamo due diagonali, una diagonale "a→d" e l' altra diagonale "c→b".

La regola dice:

facciamo il prodotto tra i due elementi della prima diagonale e poi togliamo il prodotto tra i due elementi della seconda diagonale.

Qui sotto, nella Fig. 4.1, puoi vedere l' applicazione di questa semplice regola per trovare il determinante richiesto dal nostro esercizio:

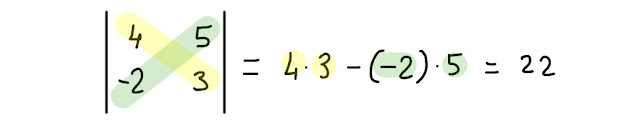Fig. 4.1 applicazione della regola per calcolare il determinante di una matrice 2 x 2

Esercizio 2

Risolvi questo sistema di equazioni fratte:

Fig 1.2 sistema numerico fratto assegnato

Svolgimento Es. 2

Come prima cosa, dobbiamo controllare le condizioni di esistenza (C. E.). 

Dobbiamo imporre che

y ≠ 0, x ≠ 0, y ≠ 2

Perché imponiamo queste condizioni?

Perché i denominatori presenti nel sistema non possono annullarsi.

Non si può dividere per zero, giusto?

Andiamo avanti facendo delle manipolazioni algebriche che puoi seguire qui sotto nella fig. 2.2:

Fig 2.2 manipolazioni algebriche

 Ora, prendiamo l' espressione della x ottenuta dalla prima equazione del sistema e la mettiamo al posto della x nella seconda equazione (metodo di sostituzione).

Puoi seguire i passaggi qui sotto nella fig. 3.2:

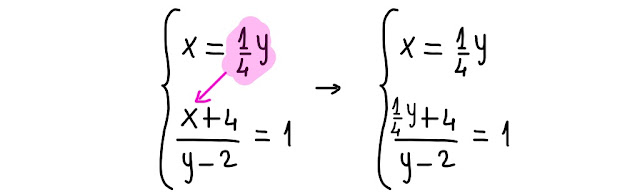Fig 3.2 ancora manipolazioni algebriche

A questo punto, risolviamo la seconda equazione del sistema, che dopo la sostituzione si è ridotta ad un' equazione nella sola incognita y.

Segui i passaggi qui sotto (fig 4.2 e fig 5.2):

Fig 4.2 risoluzione della seconda equazione del sistema (primi passaggi)

Andiamo avanti:

Fig 5.2 risoluzione della seconda equazione del sistema (ultimi passaggi)

Una volta trovato il valore della y, lo mettiamo nell' espressione della x e calcoliamo:

x = (1/4)⋅y

x = (1/4)⋅8 = 2

Ti faccio notare che sia x=2 sia y=8 rispettano le C. E., dunque sono valori accettabili.

Abbiamo così trovato la soluzione del sistema assegnato:

la coppia (2, 8).

Infatti, x=2 e y=8 soddisfano entrambe le equazioni del sistema.

Verifica con dei conticini facili!