Esercizio 1
Risolvi e discuti questo sistema letterale intero, in cui x ed y sono le incognite e a è il parametro che viaria nell' insieme dei numeri reali (a ∈ R):
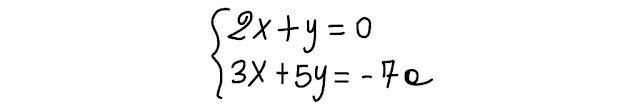 |
| Fig. 1.1 sistema letterale intero assegnato |
Svolgimento Es. 1
Scriviamo le due equazioni del sistema assegnato in forma esplicita:
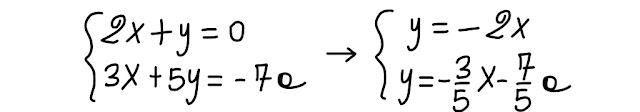 |
| Fig. 2.1 manipolazione algebrica |
Esse rappresentano le equazioni di due rette.
Possiamo notare che per ogni valore reale del
parametro a (∀ a ∈ R) le due rette sono incidenti, quindi il sistema possiede una sola soluzione (il sistema è determinato).
Andando avanti, si ha:
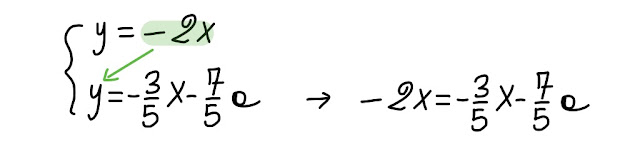 |
| Fig. 3.1 manipolazione algebrica: sostituzione |
Risolvo l' equazione di primo grado nell' incognita x ottenuta dopo la sostituzione:
 |
| Fig. 4.1 risoluzione dell' equazione di primo grado nell' incognita x |
 |
| Fig. 5.1 soluzione dell' equazione di primo grado nell' incognita x |
Di conseguenza, y = -2a
La soluzione del sistema è data dalla coppia (a, -2a)
Esercizio 2
Risolvi e discuti questo sistema letterale fratto, nelle incognite x ed y e parametro b ∊ R:
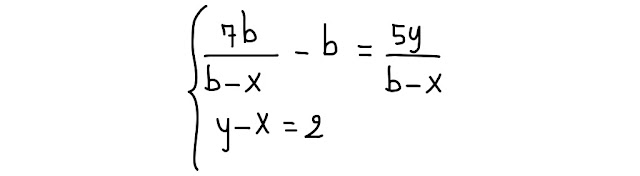 |
| Fig. 1.2 sistema letterale fratto assegnato |
Svolgimento Es. 2
Discutere questo sistema letterale significa studiare cosa succede al variare del parametro b.
Osservando il denominatore, b-x, della prima equazione, devo imporre che esso sia diverso da zero, dunque
b≠x .
Ora moltiplico primo e secondo membro della prima equazione del sistema per b-x, ottenendo un' equazione equivalente alla prima equazione del sistema assegnato:
 |
| Fig. 2.2 manipolazione della 1^ equazione del sistema |
Dalla seconda equazione del sistema assegnato si ha che
y = x+2.
Adesso metto l' espressione x+2 nella y dell' equazione di Fig. 2.2 (metodo di sostituzione):
 |
| Fig. 3.2 manipolazione algebrica: sostituzione |
Vado avanti e semplifico:
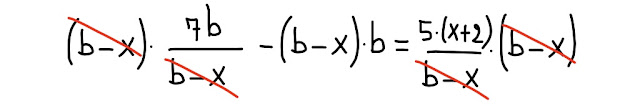 |
| Fig. 4.2 manipolazione algebrica: semplificazione |
Se b ≠ 5, allora x = b-2.
Siccome y = x + 2,
y = b - 2 + 2 = b
La soluzione è quindi data dalla coppia (b-2, b)
Se b ≠ 5, il sistema è determinato.
∀ b ∈ R ( b ≠ 5 ), notiamo che
x = b - 2 rispetta la condizione x ≠ b
Se invece b = 5, il sistema assegnato diventa:
 |
| Fig. 6.2 metodo di sostituzione |
Dopo la sostituzione, si ha
35 - 25 + 5x = 5(x+2)
10 + 5x = 5x + 10
0⋅x = 0
Questa equazione ha infinite soluzioni e dunque il sistema è indeterminato.

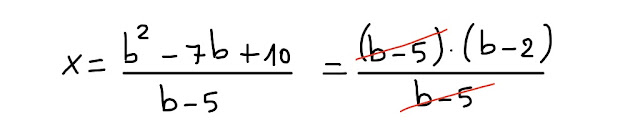










Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)