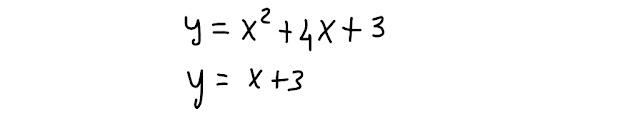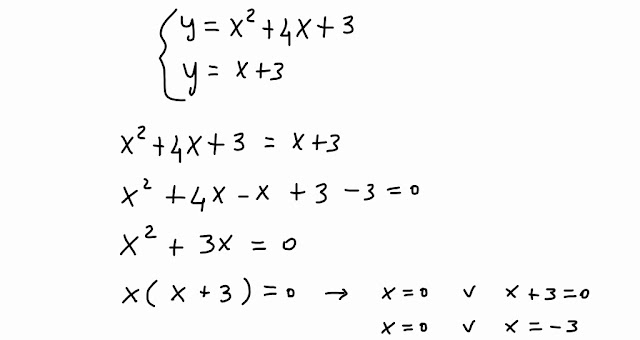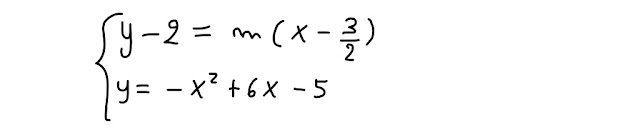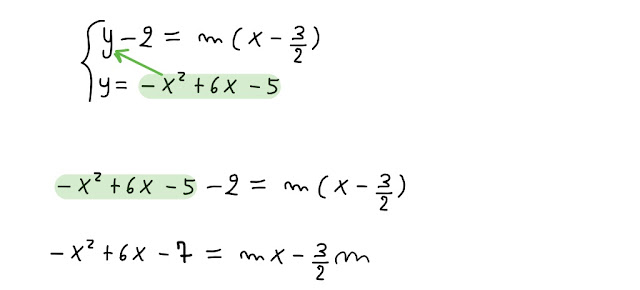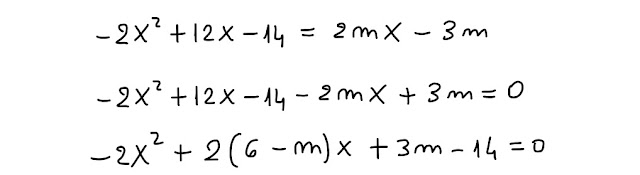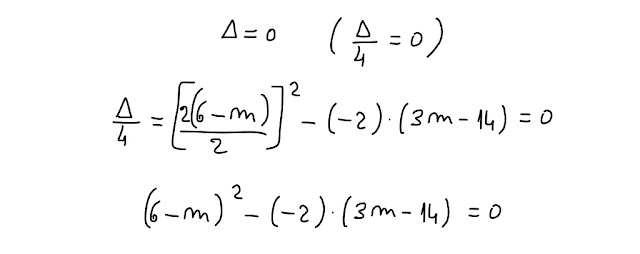In questa esercitazione, estratta dal mio Tutorial sulla Parabola, vedremo lo svolgimento di 2 esercizi di matematica per le Superiori.
Imparerai come si trovano le eventuali intersezioni tra una parabola ed una retta ed anche come si trovano le rette tangenti ad una parabola condotte da un punto.
Ex. 1
Scopri gli eventuali punti di intersezione tra la parabola e la retta assegnate:
Risolviamo questo sistema:
Le soluzioni che abbiamo trovato sono reali e distinte, quindi avremo due punti di intersezione distinti tra loro.
A questo punto, calcoliamo i valori di y corrispondenti:
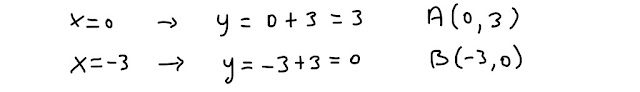 |
Le coppie (x,y), soluzioni del sistema che abbiamo trovato, rappresentano le coordinate dei punti in comune tra la retta e la parabola.
|
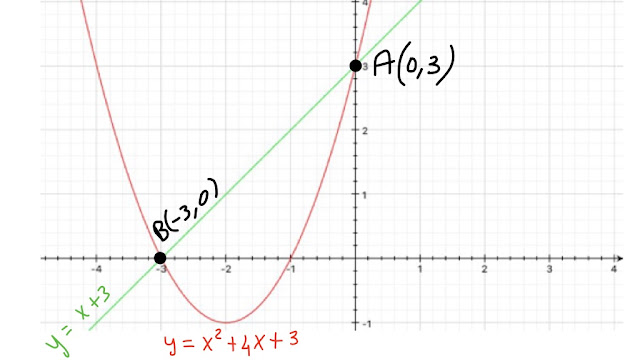
Questi punti stanno sia sulla retta sia sulla parabola, sono appunto i punti di intersezione tra il grafico della parabola e quello della retta (vedi figura qui sotto).
Andiamo avanti col secondo esercizio.
Ex. 3
Scrivi le equazioni delle rette tangenti, condotte dal punto (3/2, 2), alla parabola
 |
Scriviamo l' equazione della retta generica passante per il punto assegnato:
Ora mettiamo a sistema l' equazione di questa generica retta passante per il punto assegnato con l' equazione della parabola:
Manipoliamo e andiamo avanti col sistema:
Moltiplico per 2 entrambi i membri dell' ultima equazione scritta:
A questo punto, "scatta" la condizione di tangenza:
Sviluppo il quadrato del binomio e vado avanti con l' ultima equazione scritta:
Ecco, come vedi, la condizione di tangenza ci ha condotto ad un' equazione di secondo grado nell' incognita m, che, una volta risolta, ci fornirà i valori di m coi quali "costruiremo" le equazioni delle
rette tangenti cercate. Risolviamo l' ultima equazione che ho scritto:
Ciascuno dei due valori trovati verrà messo nella formula della retta generica passante per il punto assegnato.
Facendo i conti, si trovano le equazioni delle rette tangenti che l' esercizio ci ha chiesto:
Nel grafico qui sotto è possibile vedere la parabola e le due rette tangenti ad essa, condotte dal punto P assegnato.
👇👇👇
Scopri di più
Se vuoi ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.
Se hai dubbi, osservazioni, non esitare a lasciare un commento qui sotto ✍✍✍