Ultimo aggiornamento: 25/02/2021
In questa esercitazione vedremo:
come si disegnano i grafici di funzioni particolari;
come si disegnano i grafici con archi di coniche.
1) y = - √(1 - 16x²)
2) y = 1 - √[4x(x+4)]
Troverai:
⚫ come si determina il dominio di queste due funzioni;
⚫ come si risolve una particolare disequazione del tipo
A(x)・B(x) ⋛ 0;
⚫ come si applica il metodo del completamento del quadrato.
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.

In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
Esercizio 1
Vogliamo disegnare il grafico di questa funzione:
 |
Come prima cosa, bisogna determinarne il dominio.
Dobbiamo imporre che il radicando sia maggiore o uguale a zero.
Dunque la funzione ha senso per tutti quei valori di x compresi tra -1/4 e 1/4, estremi inclusi.
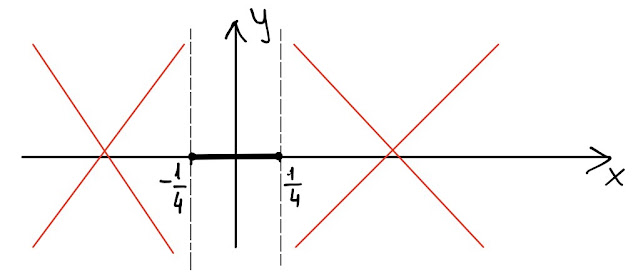 |
| Fig. 1 |
Come si intuisce dalla figura 1, il grafico della funzione assegnata si trova solo all' interno del "corridoio" che va da -1/4 a 1/4, estremi inclusi.
E poi c' è da dire un' altra cosa importante:
y = -√(1 - 16x²)
è minore o uguale a zero, per ogni x del suo dominio.
Perché?
Perché la radice quadrata restituisce qualcosa che è maggiore o uguale a zero, che col segno meno davanti diventa minore o uguale a zero.
Quindi nel "corridoio" di Fig. 1, cioè nell' intervallo [-1/4, 1/4], il grafico della nostra funzione si troverà non sopra ( ≤ 0 ) l' asse delle ascisse.
E' per questo motivo che adesso ricorro alla figura 2 seguente che mostra quali sono tutte le porzioni del piano cartesiano, quelle coi freghi rossi, dove il grafico non giacerà:
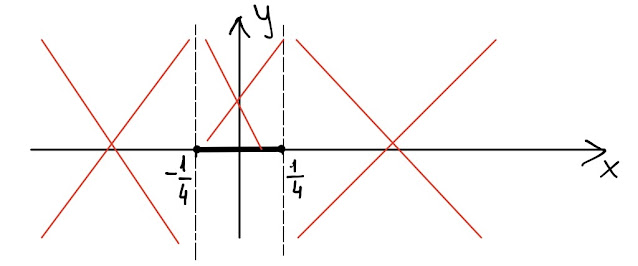 |
| Fig. 2 |
Andiamo avanti!
Bene, torniamo all' esercizio!
Confrontando, si ha:
Questa è una disequazione di 2° grado che potremmo risolvere calcolando il Delta(Δ) dell' equazione associata, poi trovando le eventuali radici reali e infine disegnando la parabola per vedere in quali intervalli la disequazione è soddisfatta. Prova a fare così.
Si tratta di due semplici disequazioni, che risolviamo:
Eleviamo al quadrato 1° e 2° membro dell' equazione della funzione e otteniamo:
Quest' ultima è l' equazione di quale curva?
Ti dice qualcosa?
Prima di andare avanti, ci tengo a dirti che puoi imparare di più attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è
Matematica Quinquennio
Se vuoi scoprire di più e iniziare un percorso, fai click sul link qui sotto:
Bene, torniamo all' esercizio!
Dicevo:
ti dice qualcosa l' equazione
16x² + y² = 1 ?
Si tratta di un' ellisse!
Infatti, possiamo riscrivere l' ultima equazione trovata anche nel seguente modo:
Che cosa ti ricorda l' equazione scritta così?
L' equazione adesso è scritta nella forma canonica dell' equazione di una ellisse centrata nell' origine degli assi cartesiani e riferita proprio agli assi x ed y:
Confrontando, si ha:
Ora, tenendo conto del fatto che y = -√(1 - 16x²) ≤ 0 per ogni x del suo dominio, disegneremo la parte di ellisse che non si trova sopra l' asse x, perché quello è il grafico che cerchiamo, cioè il grafico dell' ellisse i cui punti hanno ordinata minore o uguale di zero.
L' equazione, senza tener conto della limitazione sulla y, ci dà un' ellisse centrata nell' origine degli assi cartesiani, avente semiasse minore, a, di lunghezza 1/4 e semiasse maggiore, b, di lunghezza 1 (Fig. 3).
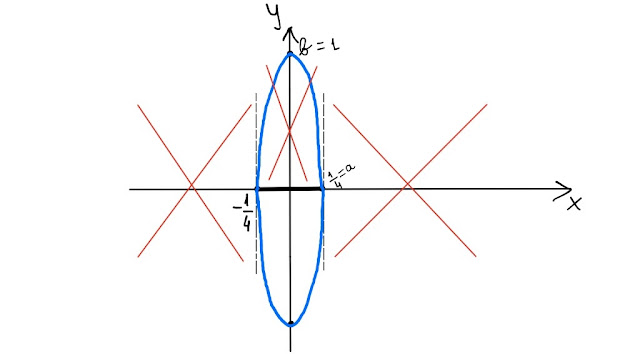 |
| Fig. 3 |
Siccome la y della nostra funzione è minore o uguale di zero, il diagramma richiesto è il seguente:
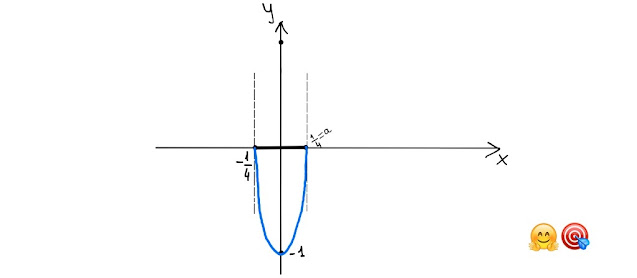 |
| Fig. 4 |
Infatti tutti i punti di questa semi-ellisse (Fig. 4) hanno ordinata y minore o uguale a zero.
Esercizio 2
Vogliamo disegnare il grafico di questa seconda funzione, che rispetto alla prima, proposta nel 1° esercizio, presenta qualche difficoltà in più:
Come prima cosa, bisogna determinarne il dominio.
Dobbiamo imporre che il radicando sia maggiore o uguale di zero:
Questa è una disequazione di 2° grado che potremmo risolvere calcolando il Delta(Δ) dell' equazione associata, poi trovando le eventuali radici reali e infine disegnando la parabola per vedere in quali intervalli la disequazione è soddisfatta. Prova a fare così.
Qui in questo post seguiamo un' altra via:
studiamo il segno del fattore
4x
ed anche del fattore
x+4.
Poniamo entrambi i fattori maggiori di zero:
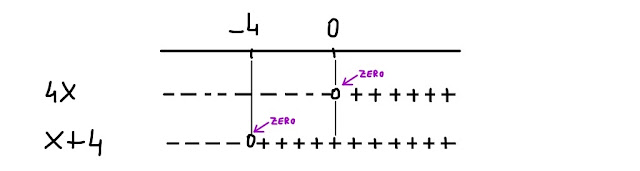
Il 1° fattore, 4x, è positivo per x > 0;
il 2° fattore, x + 4, è positivo per x > -4
Visualizziamo attraverso il grafico dei segni queste informazioni:
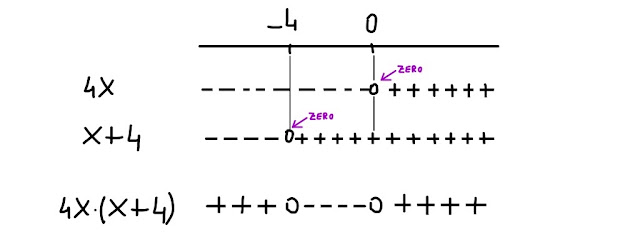
Una volta rappresentate le linee dei segni relative ai due fattori, abbiamo bisogno di rappresentare una terza linea: quella dedicata al prodotto dei due fattori, che trovi in basso nel seguente disegno:
Riprendiamo l' equazione della nostra funzione e la scriviamo isolando la radice quadrata:
Nell' intervallo (-∞, -4), 4x è negativo e x+4 è anch' esso negativo, dunque il loro prodotto è positivo.
Nell' intervallo (-4, 0), 4x è negativo e x+4 è positivo, dunque il loro prodotto è negativo.
Nell' intervallo ( 0, +∞), 4x è positivo e x+4 è anch' esso positivo, dunque il loro prodotto è positivo.
E in corrispondenza dei capisaldi?
Per x = -4, 4x è negativo e x+4 è nullo, dunque il loro prodotto vale zero.
Per x = 0, 4x è nullo e x+4 è positivo, dunque il loro prodotto è zero.
Poiché vogliamo che il prodotto dei due fattori sia maggiore o uguale a zero, 4x(x+4) ≥ 0, andiamo a considerare i segni più (+), compresi gli zeri, nella linea dei segni dedicata appunto al prodotto dei due fattori.
In corrispondenza di quali intervalli questo prodotto è positivo o nullo?
Per x ≤ -4 oppure per x ≥ 0.
Dunque il Dominio (D) è dato da
A questo punto, possiamo dire che il primo membro, y-1, è minore o uguale a zero, nel dominio della funzione.
Perché y-1 è minore o uguale a zero?
Beh, lo abbiamo già detto:
perché la radice quadrata restituisce qualcosa che è maggiore o uguale a zero, che col segno meno davanti, anche in questo esercizio, diventa minore o uguale a zero.
Adesso eleviamo al quadrato 1° e 2° membro dell' equazione della funzione, facciamo un po' di "algebra", e si ha:
Se riscriviamo in una forma migliore l' ultima equazione, si ottiene
Che cosa rappresenta l' equazione appena scritta?
Bene, rispondiamo a questa domanda sfruttando il cosiddetto
Bisogna "fare emergere" i quadrati di due binomi. Perché?
Per approfondire il metodo del completamento del quadrato, ti consiglio di studiare su questo libro:
Matematica per le Scuole superiori, con Maths in english ed espansione online e DVD-ROM(vol 3)
L' espressione tra parentesi tonde nel primo membro della seguente equazione, che è equivalente alla precedente equazione che ho scritto, è il quadrato di un binomio:
Come possiamo "pescarlo"?
Può l' espressione 4x²+16x essere un quadrato di binomio?
Il quadrato di un binomio genera tre termini (tre monomi), e l' espressione 4x²+16x presenta solo due termini!
Il terzo termine mancante (rappresentato dai puntini rossi qui sotto) che aggiungeremo al primo membro della prossima equazione verrà aggiunto anche al secondo membro, visto che 1° e 2° membro devono essere uguali.
Che cosa mettiamo al posto dei puntini rossi affinché
Bene, rispondiamo a questa domanda sfruttando il cosiddetto
metodo del completamento del quadrato.
Bisogna "fare emergere" i quadrati di due binomi. Perché?
Per approfondire il metodo del completamento del quadrato, ti consiglio di studiare su questo libro:
Matematica per le Scuole superiori, con Maths in english ed espansione online e DVD-ROM(vol 3)
L' espressione tra parentesi tonde nel primo membro della seguente equazione, che è equivalente alla precedente equazione che ho scritto, è il quadrato di un binomio:
Come vedi, il primo quadrato è stato trovato:
y²-2y+1 = (y - 1)²
E ora, dov' è il 2° "quadrato"?
Come possiamo "pescarlo"?
Può l' espressione 4x²+16x essere un quadrato di binomio?
Il quadrato di un binomio genera tre termini (tre monomi), e l' espressione 4x²+16x presenta solo due termini!
Il terzo termine mancante (rappresentato dai puntini rossi qui sotto) che aggiungeremo al primo membro della prossima equazione verrà aggiunto anche al secondo membro, visto che 1° e 2° membro devono essere uguali.
(4x² + 16x + ...)
4x² è il quadrato di 2x.
Costruiamo questo quadrato di binomio che stiamo cercando:
( 2x + ... )² = 4x² + 16x + ...
Siccome il termine dato dal doppio prodotto del 1° termine ( 2x )
Costruiamo questo quadrato di binomio che stiamo cercando:
( 2x + ... )² = 4x² + 16x + ...
Siccome il termine dato dal doppio prodotto del 1° termine ( 2x )
per il 2° (...) deve essere
16x, abbiamo che
2(2x)(...) = 16x ⟶
2(2x)(...) = 16x ⟶
(segue che)⟶ al posto di
... mettiamo un bel 4 e al posto di
Ora, se aggiungiamo una quantità al 1° membro, dobbiamo aggiungere la stessa quantità al 2° membro, per ottenere un' equazione equivalente.
Nello specifico, aggiungiamo 16:
Nello specifico, aggiungiamo 16:
In questo modo, otteniamo 1 al 2° membro e l' equazione assume la forma, forse più facilmente riconoscibile, dell' equazione di
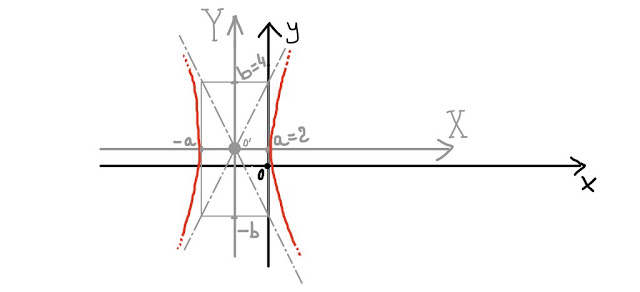
Così facendo, l' equazione assume proprio la forma canonica dell' equazione di un' iperbole, con centro di simmetria O', riferita al sistema O'XY, che puoi vedere nella prossima figura.
Bene, abbiamo tutti gli ingredienti per disegnare l' iperbole, riferendola al sistema O'XY, che però NON è proprio il grafico che cerchiamo.
Comunque disegniamo il grafico (in rosso) dell' iperbole e poi terremo conto della limitazione sulla y (minuscola!):
Comunque disegniamo il grafico (in rosso) dell' iperbole e poi terremo conto della limitazione sulla y (minuscola!):
Dobbiamo pertanto considerare SOLO la parte di grafico dell' iperbole i cui punti, riferiti questa volta al sistema Oxy, hanno ordinata y ≤ 1.
Nella figura che segue abbiamo il grafico che stavamo cercando:

Nella figura che segue abbiamo il grafico che stavamo cercando:
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!

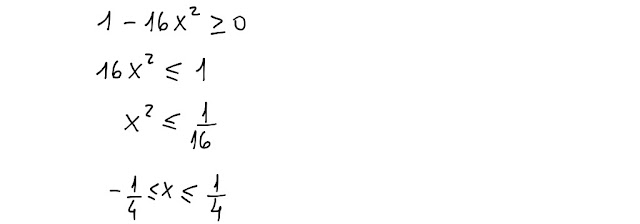
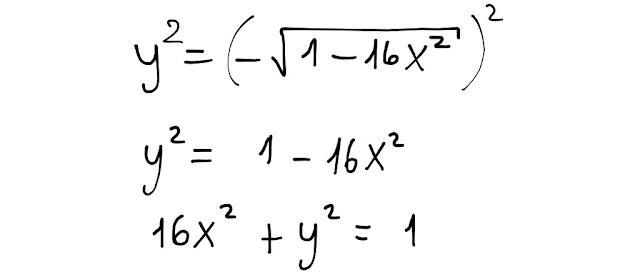
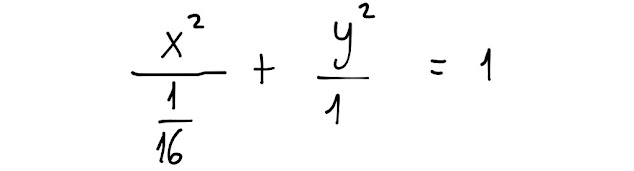
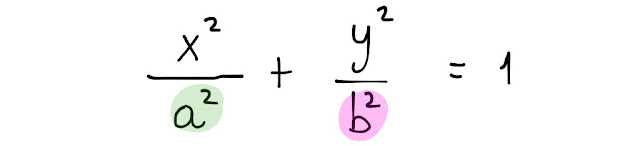
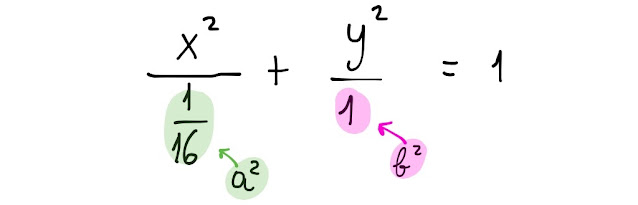
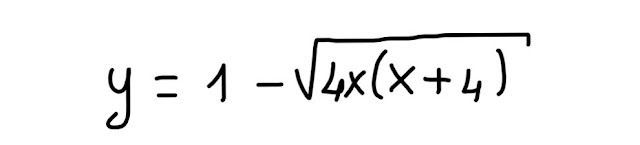
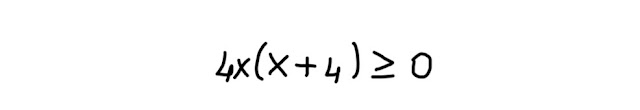
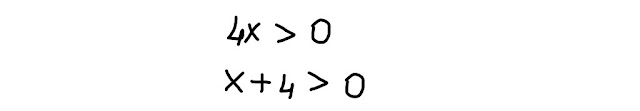

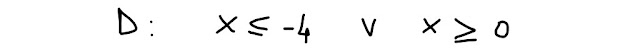
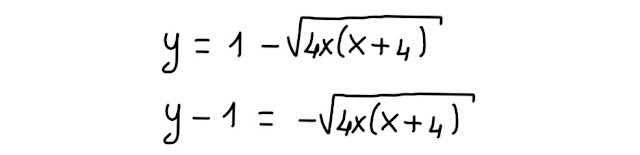
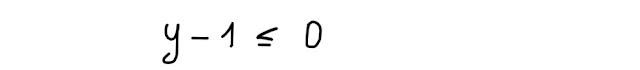
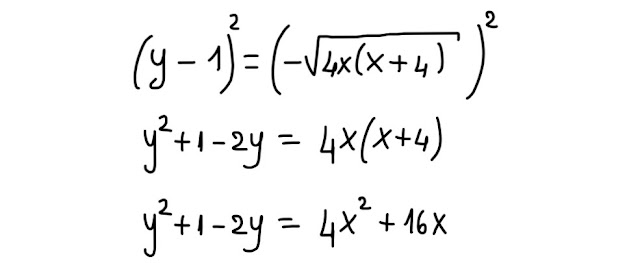
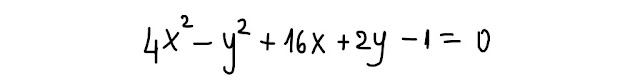
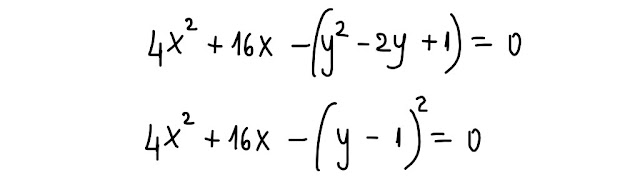
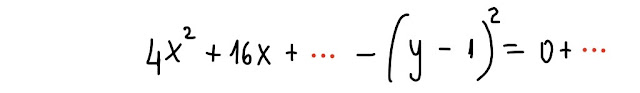

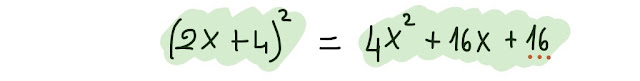
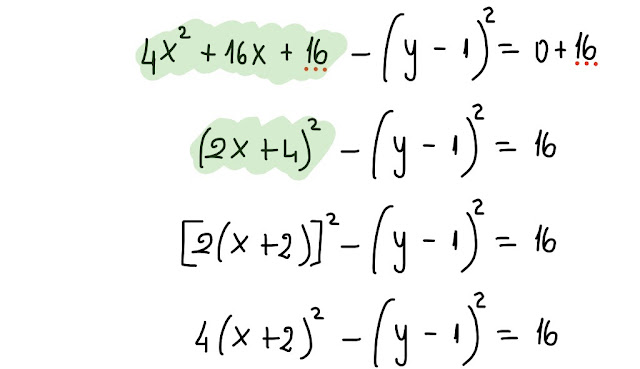
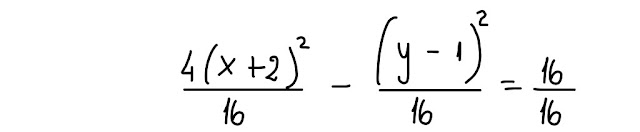

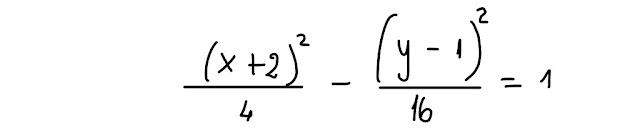
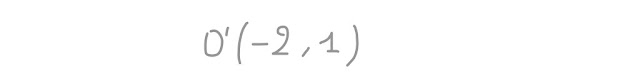
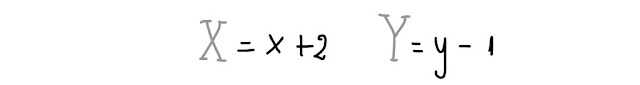
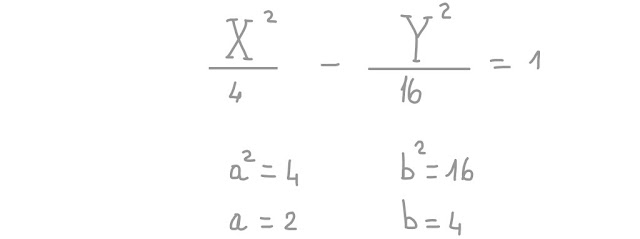
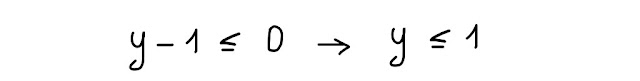











Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)