Disequazioni di secondo grado: come si risolvono

Ultimo aggiornamento: 03/03/2021

Fig. 1

In questa esercitazione, vedremo

come si risolve una disequazione.

In particolare, vedremo

come si risolve una disequazione di secondo grado

del tipo

A(x)⋅B(x)⋛0

(dove A(x) e B(x) sono polinomi di primo grado)

Ciao! Sono Giuseppe.
In questo blog pubblico

esercizi svolti di matematica

per le scuole superiori e l' università.

Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
 

Esercizio

Risolvi questa disequazione:

(2x+1)(x-7)<0

Svolgimento

Studiamo il segno di ciascun fattore, prendendoci la libertà di seguire una via leggermente diversa da quella solita:

1° fattore

👇

2x+1<0

(Ecco una novità, se così la possiamo chiamare: invece di porre il primo fattore maggiore di zero, lo abbiamo posto minore di zero; semplicemente invece di chiederci dove questo fattore è positivo, ci domandiamo dove è negativo)

2° fattore

👇

x-7>0

(qui invece mi sono preso la "libertà" ☺️ di porre il secondo fattore maggiore di zero, come normalmente si fa)

Risolviamo queste due semplici disequazioni:

2x+1<0 ➝ x<-1/2

x-7>0 ➝ x>7

Prima di andare avanti, ci tengo a dirti che puoi imparare di più attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è

Matematica Quinquennio

Se vuoi scoprire di più e iniziare un percorso gratuito, fai click sul link qui sotto:

iscriviti gratis qui.

Bene, torniamo all' esercizio!

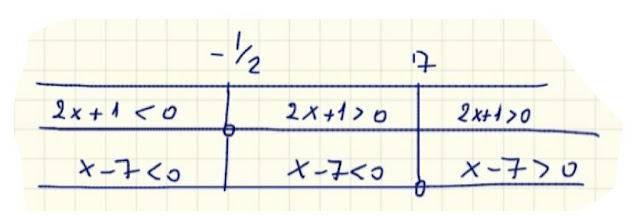
Visualizziamo queste informazioni sui segni dei due fattori:

Fig. 2

Il primo fattore, 2x+1, è negativo per

x<-1/2, è positivo per 

x>-1/2, ed è nullo per

x=-1/2

Il secondo fattore, x-7, è positivo per

x>7, è negativo per 

x<7, ed è nullo per

x=7

Siccome 

(2x+1)(x-7)<0 ,

occorre considerare gli intervalli in cui i due fattori hanno segni diversi, perché il loro prodotto deve essere strettamente minore di zero.

Quali sono gli intervalli in cui il prodotto dei due fattori è minore di zero?

Guardando la fig. 2, scopriamo che solo in un intervallo i due fattori hanno segni diversi e il loro prodotto è negativo: mi riferisco all' intervallo

-1/2<x<7

Concludo dicendo che tutti i valori reali maggiori di -1/2 e minori di 7 soddisfano la disequazione assegnata.

Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto: 

troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.

Alla prossima lezione. Ciao, ti aspetto!