Cosa sono le coordinate polari?
Come si scrive l' equazione di una retta in coordinate polari?
Come si disegna una retta a partire dalla sua equazione in forma polare?
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 3 esercizi svolti.
Ricordiamo velocemente cosa sono le coordinate polari e come possono aiutare a individuare un punto sul piano.
 |
| Fig. 1 |
Il punto P che vediamo sul piano nella fig. 1 può essere individuato anche da coordinate diverse da quelle cartesiane.
P ha una distanza r dal punto di intersezione O degli assi cartesiani (che possiamo far coincidere col cosiddetto polo del sistema polare) e il segmento OP forma un angolo α col semiasse positivo delle ascisse (che possiamo far coincidere col cosiddetto asse polare).
Ogni punto P del piano della fig. 1 è individuabile dalla sua distanza r dal polo O e dall' angolo α che il segmento OP forma con l' asse polare.
r si chiama modulo ed α viene detto argomento.
Ecco le relazioni che intercorrono tra le coordinate polari di un punto P e le sue coordinate cartesiane:
P(r, α), P(x, y)
x=r⋅cosα
y=r⋅sinα
Adesso vediamo un altro modo per individuare una qualunque retta giacente sul piano e non passante per l' origine.
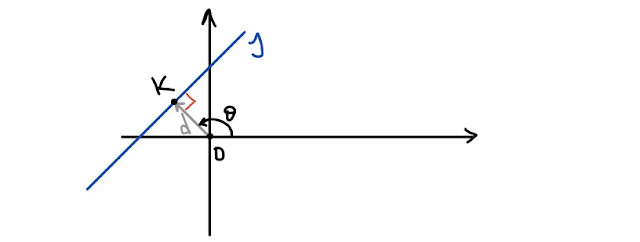
Ogni retta del piano non passante per l' origine ha una sua distanza d dal polo O e il segmento orientato OK (K è il punto di intersezione tra la retta e la sua perpendicolare passante per O) forma un angolo θ con l' asse polare.
Osserva le figure 2, 3 e 4.
 |
| Fig. 2 |
 |
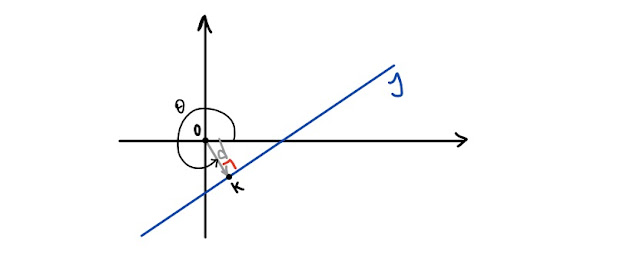
| Fig. 3 |
 |
| Fig. 4 |
Bene! Forti di queste considerazioni, scopriamo come si scrive, in coordinate polari, l' equazione di una retta del piano non passante per l' origine.
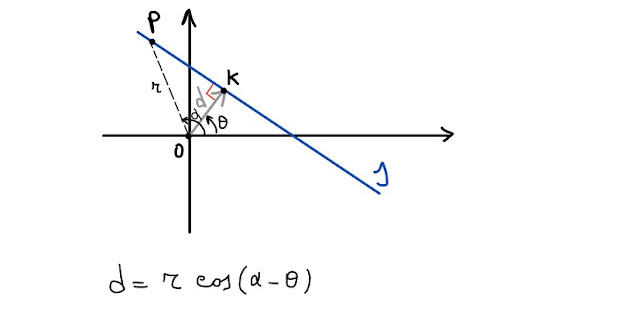 |
| Fig. 5 |
Osservando la fig. 5, in particolare il triangolo rettangolo OKP, possiamo scrivere che il cateto OK, la cui lunghezza è d, è uguale al prodotto dell' ipotenusa, r, per il coseno dell' angolo adiacente (adiacente al cateto OK).
L' angolo adiacente è α-θ (fig. 5)
Equazione di una retta in coordinate polari
Dunque l' equazione, in forma polare, di una retta non passante per l' origine è:
d=r⋅cos(α-θ)
Ti faccio notare che, siccome il coseno è una funzione goniometrica pari, possiamo anche scrivere
d=r⋅cos(θ-α)
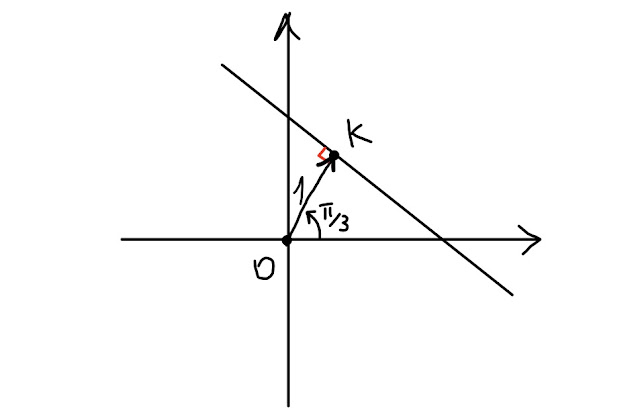
Qui sotto, nella fig. 6, puoi vedere un esempio particolare di retta che dista 4 dal polo O e il cui segmento orientato OK forma con l' asse polare un angolo di π/3 radianti.
 |
| Fig. 6 |
Esercizi svolti sulle coordinate polari
Iniziamo a svolgere gli esercizi.
Esercizio 1
Trova l' equazione di una retta che forma con l' asse polare un angolo di 5π/6 e dista 2 dal polo.
Svolgo
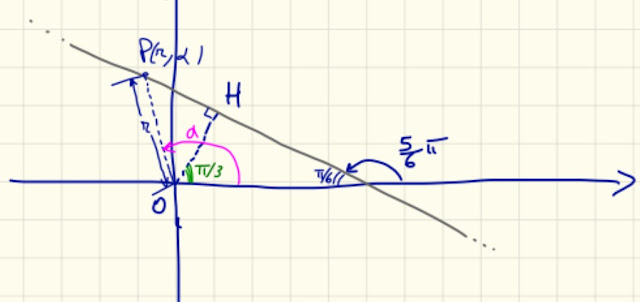
Nella figura qui sotto, disegno una delle rette possibili. Perché? Lo vedremo tra un po'.
Qui dobbiamo fare attenzione!
L' angolo di cui parla il testo dell' esercizio è l' angolo che la retta forma con l' asse polare, non l' angolo che forma il suo segmento orientato OH con l'asse polare.
Osservando la figura 7 e giocando con la geometria del problema, è facile ricavare l' angolo θ (indicato in verde nella fig. 7).
Riprendiamo l' equazione in forma polare di una retta generica non passante per l' origine:
d=r⋅cos(θ-α)
Quanto vale d ?
d=2
Quanto vale θ, secondo la figura 7 ?
θ=π/3
Equazione di una retta in forma polare
Quindi, sostituendo, abbiamo l' equazione richiesta:
2=r⋅cos(π/3-α)
La domanda che voglio farti adesso è : c' è un' altra retta che dista 2 dal polo e forma con l' asse polare un angolo di 5π//6?
La risposta è sì, e la puoi guardare nella fig. 8 qui sotto:
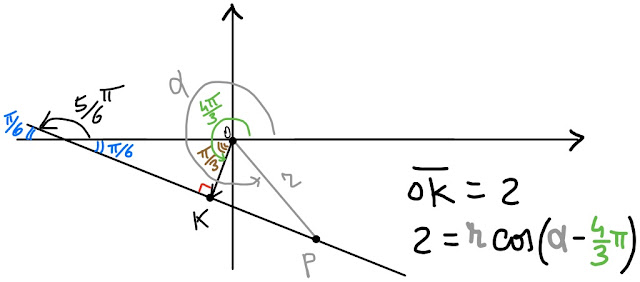 |
| Fig. 8 |
Le due rette ottenute sono parallele tra loro, entrambe distano 2 dal polo, ma hanno differenti angoli formati dai loro rispettivi segmenti orientati OK con l' asse polare.
Esercizio 2
Sia
r⋅sin(π/6-α)=3
l' equazione polare di una retta. Si chiede di disegnarla e di trovare la sua equazione cartesiana.
Svolgo
Abbiamo visto in questo tutorial che la forma polare dell' equazione di una retta non passante per l' origine è questa:
d=r⋅cos(α-θ)
Beh, l' equazione della retta assegnata non è proprio in quest' ultima forma!
Come si fa?
Andiamo a chiedere un favore agli archi associati,☺️
che molto gentilmente ci danno una mano.
Sappiamo che
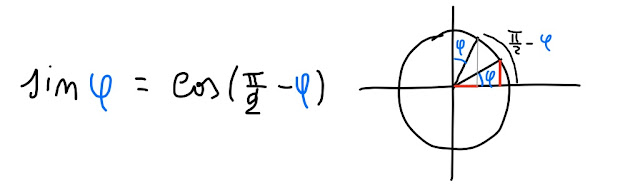 |
| Fig. 9 |
Perché ti ho fatto vedere questo?
Perché vogliamo trasformare sin(π/6-α) della nostra equazione assegnata nella forma
cos(α-θ).
Ora, il nostro angolo φ, che vediamo in fig. 9, è
π/6-α.
Seguendo la relazione che ho scritto in fig. 9, abbiamo che
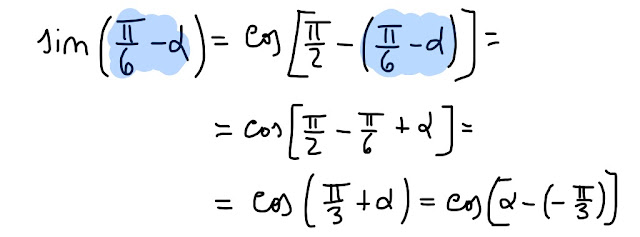 |
| Fig. 10 |
Wow! Meraviglia delle meraviglie, abbiamo la possibilità di riscrivere l' equazione della retta assegnata nella forma che volevamo.
Eccola:
r⋅sin(π/6-α)=3
 |
| Fig. 11 |
3 è la distanza della retta dal polo O.
θ=-π/3 è l' angolo (negativo perché percorso in senso orario) formato dal segmento orientato OK e l' asse polare.
Con questi due valori, d e θ, abbiamo potuto disegnare la retta cercata (fig. 11).
Per ottenere l' equazione nella forma cartesiana, possiamo sviluppare, sfruttando la formula di sottrazione del seno, l' equazione assegnata all' inizio dell' esercizio:
r⋅sin(π/6-α)=3
 |
| Fig. 13 |
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
👇👇👇
Segui la lezione sul mio Canale Youtube:


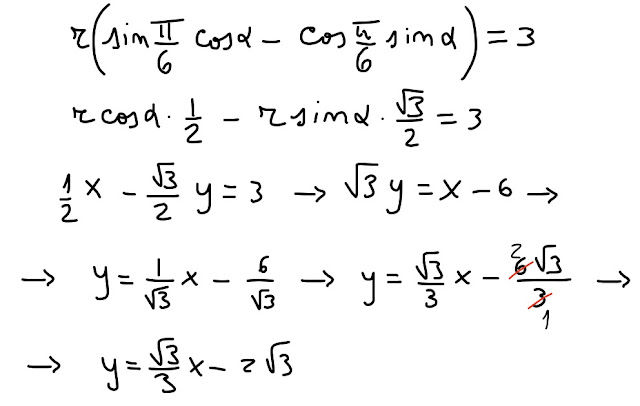










Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)