 |
| Fig. 0 |
Come si fa la divisione tra due polinomi a coefficienti numerici?
Come si fa la divisione tra due polinomi a coefficienti letterali?
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi svolti.
Divisione tra polinomi
Esercizio 1
Esegui la
divisione tra due polinomi:
 |
| Fig. 1 |
Svolgimento
Come prima cosa, occorre riscrivere in forma completa e ordinata sia il polinomio dividendo sia il polinomio divisore, per poter eseguire l'
algoritmo della divisione tra due polinomi.
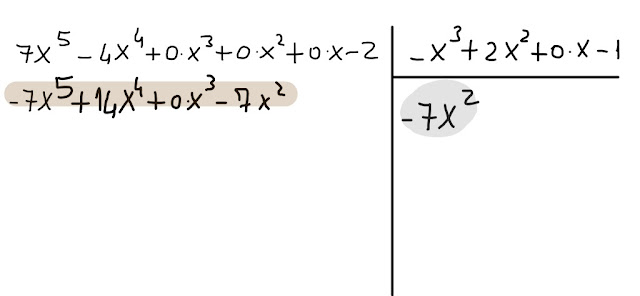 |
| Fig. 2 |
-7x² è dato dalla divisione del 1° termine del polinomio dividendo per il 1° termine del polinomio divisore.
Adesso osserviamo il polinomio che nella fig. 2 compare sotto il dividendo.
Il suo 1° termine è l' opposto del prodotto del 1° termine del polinomio quoziente per il 1° termine del divisore.
Il suo 2° termine è l' opposto del prodotto del 1° termine del polinomio quoziente per il 2° termine del divisore.
Il suo 3° termine è l' opposto del prodotto del 1° termine del polinomio quoziente per il 3° termine del divisore. Poiché viene
0⋅x³ ,
questo termine, in pratica, non ha un opposto e dunque scriviamo semplicemente...(v. fig. 2)
+0⋅x³ , proprio sotto il termine
+0⋅x³ del dividendo.
Il 4° termine del polinomio evidenziato in marrone è l' opposto del prodotto del 1° termine del polinomio quoziente per il 4° termine del divisore.
 |
| Fig. 3 |
Il polinomio verde che vediamo nella fig. 3 è dato dalla somma algebrica tra il dividendo e il polinomio evidenziato in marrone.
Il secondo termine del polinomio quoziente,
-10x , è dato dalla divisione del 1° termine del polinomio verde per il 1° termine del polinomio divisore.
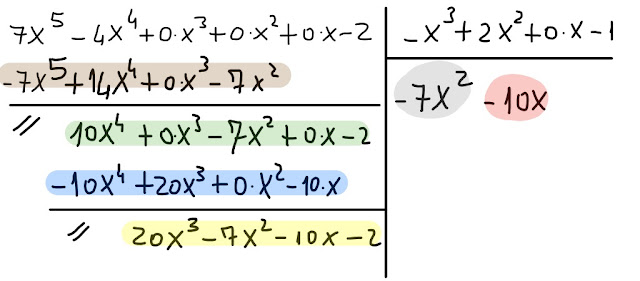 |
| Fig. 4 |
Guardiamo ora il polinomio evidenziato in celeste della fig. 4.
Il suo 1° termine è l' opposto del prodotto del 2° termine del polinomio quoziente per il 1° termine del divisore.
Il suo 2° termine è l' opposto del prodotto del 2° termine del polinomio quoziente per il 2° termine del divisore.
Il suo 3° termine è l' opposto del prodotto del 2° termine del polinomio quoziente per il 3° termine del divisore. Viene
0⋅x² ,
e dunque mettiamo semplicemente
+0⋅x² sotto il termine -7x² del polinomio verde di fig. 4
Il 4° termine del polinomio evidenziato in celeste è l' opposto del prodotto del 2° termine del polinomio quoziente per il 4° termine del divisore.
Il polinomio in giallo della fig. 4 è dato dalla somma algebrica tra il polinomio verde e il polinomio celeste.
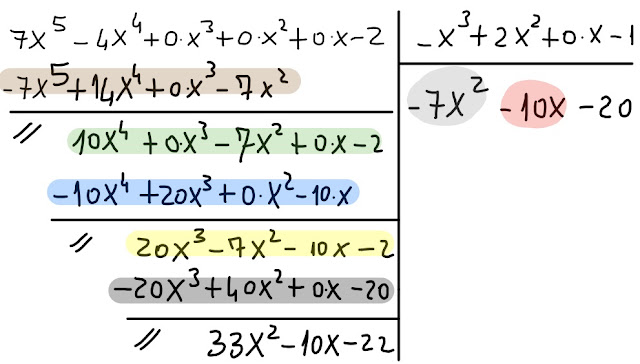 |
| Fig. 5 |
Il terzo termine del polinomio quoziente,
-20 , è dato dalla divisione del 1° termine del polinomio in giallo per il 1° termine del polinomio divisore.
Guardiamo ora il polinomio evidenziato in grigio scuro della fig. 5.
Il suo 1° termine è l' opposto del prodotto del 3° termine del polinomio quoziente per il 1° termine del divisore.
Il suo 2° termine è l' opposto del prodotto del 3° termine del polinomio quoziente per il 2° termine del divisore.
Il suo 3° termine è l' opposto del prodotto del 3° termine del polinomio quoziente per il 3° termine del divisore. Siccome il prodotto viene
0⋅x ,
mettiamo semplicemente
+0⋅x sotto il termine -10x del polinomio in giallo.
Il 4° termine del polinomio in grigio scuro è dato dall' opposto del prodotto del 3° termine del polinomio quoziente per il 4° termine del divisore.
Il polinomio
33x²-10x-22 (fig. 5 )
è dato dalla somma algebrica tra il polinomio in giallo e il polinomio in grigio scuro.
Dato che il grado di quest' ultimo polinomio è 2, che è minore del grado del divisore (3),
il polinomio resto è proprio
R(x)=33x²-10x-22 .
Il polinomio quoziente è
Q(x)=-7x²-10x-20
Questa è la
divisione con resto tra due polinomi:
 |
| Fig. 6 |
Per fare la verifica, cioè per vedere se abbiamo fatto bene i conti, il polinomio dividendo deve essere uguale alla somma tra il prodotto del polinomio divisore per il polinomio quoziente e il polinomio resto:
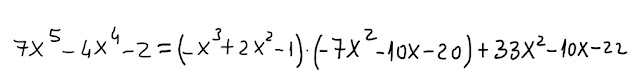 |
| Fig. 7 |
Sviluppando e semplificando il 2° membro di fig. 7, otteniamo proprio il polinomio dividendo.
Adesso passiamo al 2° e ultimo esercizio di questo tutorial.
Esercizio 2
Esegui la
divisione tra due polinomi a coefficienti letterali:
 |
| Fig. 8 |
Sia x l' indeterminata di riferimento dei due polinomi.
Svolgimento
Come abbiamo visto nell' esercizio precedente, dobbiamo eseguire l' algoritmo della divisione riscrivendo il polinomio dividendo e il polinomio divisore in modo ordinato e completo, stando, in questo caso, attenti al numero dei termini in gioco.
 |
| Fig. 9 |
Nella fig. 9 qui sopra, possiamo vedere l' algoritmo eseguito secondo il procedimento indicato nell' esercizio precedente.
Notiamo che il numero dei termini del polinomio divisore, scritto in forma completa, è n+1.
Abbiamo un
polinomio quoziente:
Q(x) = xⁿ⁺¹ - yⁿ⋅x
Osservando Q(x), ti faccio notare che -yⁿ è il coefficiente letterale di x.
E abbiamo un
polinomio resto:
R(x) = y²ⁿ⋅x + y²ⁿ⁺¹
Osservando R(x), ti faccio notare che y²ⁿ è il coefficiente letterale di x e y²ⁿ⁺¹ è il coefficiente letterale di x⁰
Perché questo R(x) è il polinomio resto?
Perché il suo grado è 1 (ti ricordo che l' indeterminata è x, non y), e 1 è minore, lo dice l' esercizio, di n (il grado del divisore).
Quindi, poiché
grado[R(x)] < grado(xⁿ+yⁿ) ,
R(x) è il polinomio resto della divisione.
Nella fig. 10 qui sotto, facciamo uno zoom sui termini del polinomio divisore, compresi quelli coi coefficienti nulli.
 |
| Fig. 10 |
Nella fig. 11 qui sotto, facciamo uno zoom anche sui termini del polinomio dividendo, compresi quelli coi coefficienti uguali a zero.
 |
| Fig. 11 |
Lo "zoom" fatto sui termini dei due polinomi, dividendo e divisore, aiuta a capire meglio perché l' algoritmo viene eseguito nel modo indicato in fig. 9.
Anche questa volta possiamo fare la verifica, cioè per vedere se abbiamo fatto bene i conti, il polinomio dividendo deve essere uguale alla somma tra il prodotto del polinomio divisore per il polinomio quoziente e il polinomio resto:
 |
| Fig. 12 |
 |
| Fig. 13 |
Evviva!!
Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
👇👇👇
Guarda questa esercitazione in video:











Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)