Retta nel Piano Cartesiano: Esercizi Svolti

Fig. 0

Noti due punti del piano cartesiano, come si trova l' equazione della retta che passa per essi?

Come si trova, o come si riconosce, il coefficiente angolare di una retta?

Come si trova, o come si individua, l' ordinata all' origine di una retta?

Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.

Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.

In questo breve tutorial, ti propongo un paio di esercizi.

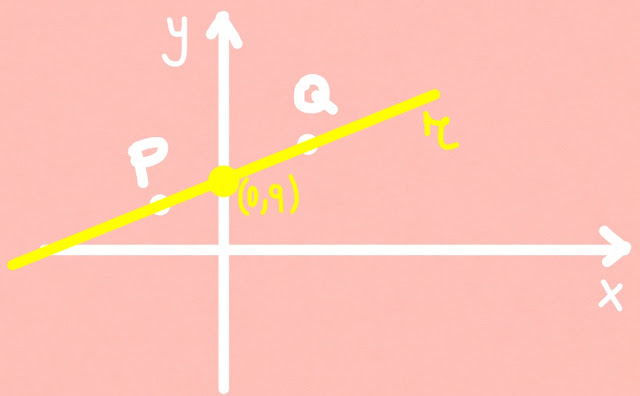
Il primo esercizio che svolgerò in questo tutorial ci fornisce due punti, P(2, 4) e Q(-1, 2), e ci chiede di trovare:

a) l' equazione della retta r passante per P e Q;

b) il coefficiente angolare della retta r;

c) l' ordinata all' origine della retta r;

d) l' equazione della retta parallela a r passante per O, l' origine degli assi cartesiani.

Svolgimento

a)
Poiché i punti assegnati ce lo permettono, utilizziamo la formula

Fig. 1

per ricavare l' equazione della retta r.

P(2, 4) sia il nostro primo punto e Q(-1, 2) il secondo punto.
Dunque x₁=2, y₁=4, x₂=-1, y₂=2

Facciamo le sostituzioni, manipoliamo ed arriviamo fino all' equazione della retta in forma esplicita:

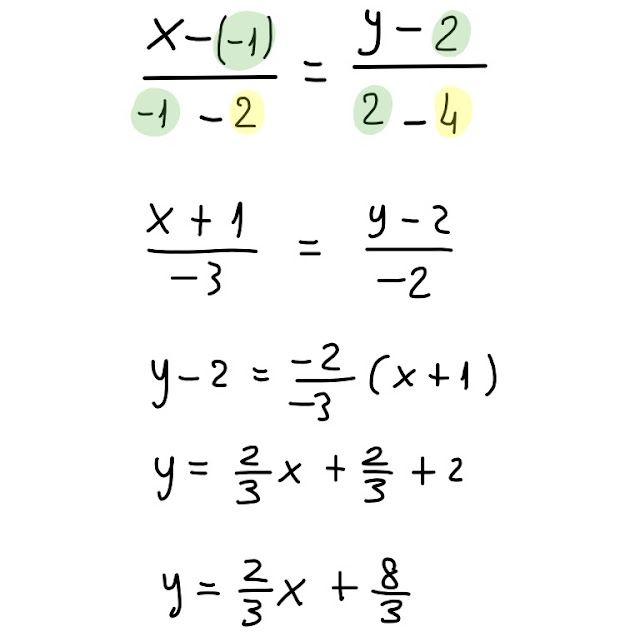Fig. 2

L' ultima che abbiamo scritto è l' equazione della retta in forma esplicita.

b)
Il coefficiente angolare è dato dal coefficiente della x nell' equazione scritta in forma esplicita, cioè 2/3

c) 
L' ordinata all' origine della retta r è data dal termine noto (quello senza lettera) nell' equazione scritta in forma esplicita, cioè 8/3

d) 
L' equazione della retta parallela a r passante per l' origine degli assi cartesiani ha la forma

y=m⋅x ,

dove m è uguale al coefficiente angolare della retta r (le due rette devono essere parallele).

Dunque

y=(2/3)x

☺️

👇👇👇

Impara di più >

👆👆👆

Il secondo esercizio che svolgerò in questo tutorial ci fornisce l' equazione in forma implicita della retta r passante per i punti P e Q,

3x+y-1=0, 

e ci chiede di trovare:

a) l' ordinata di P(2, ...) e l' ascissa di Q(... , 4) ;

b) il coefficiente angolare della retta r;

c) l' ordinata all' origine della retta r;

d) l' equazione della retta parallela a r passante per O, l' origine degli assi cartesiani.

Svolgimento

Scrivendo l' equazione nella forma esplicita, troviamo agevolmente gli elementi richiesti dai punti b), c) e d).

Ecco dunque la forma esplicita dell' equazione:

y=-3x+1

Ma prima rispondiamo al primo quesito di questo secondo esercizio.

a)
Sappiamo che P(2, yₚ) e Q(x, 4) appartengono alla retta r, quindi le loro coordinate soddisfano l' equazione della retta:

yₚ=-3⋅2+1 ⇾ yₚ=-5 ⇾ P(2, -5)

ed anche

4=-3x+1 ⇾ x = -1 ⇾ Q(-1, 4)

b)
Il coefficiente angolare è dato dal coefficiente della x nell' equazione scritta in forma esplicita, cioè -3

c) 

L' ordinata all' origine della retta r è data dal termine noto (quello senza lettera) nell' equazione scritta in forma esplicita, cioè 1

d) 

L' equazione della retta parallela a r passante per l' origine degli assi cartesiani ha la forma

y=m⋅x ,

dove m è uguale al coefficiente angolare della retta r (le due rette devono essere parallele).

Dunque

y=-3x    ☺️

Se ti è piaciuto questo tutorial di matematica, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto: 

troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.

Alla prossima lezione. Ciao, ti aspetto!

👇👇👇

Impara di più >

👆👆👆

Guarda l' esercitazione in questo video: