Come si applica la Regola di Ruffini nella divisione tra polinomi?
Vedremo la divisione in cui il polinomio divisore è del tipo x+a (a∊R) e quella in cui il polinomio divisore ha la forma b⋅x+c (b, c ∊ R, b≠1)
Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi, che svolgo e commento.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi, che svolgo e commento.
Questa esercitazione è anche disponibile in PDF stampabile, sempre a portata di mano e consultabile tutte le volte che vuoi:
divisione tra polinomi:
Siccome il divisore è del tipo x+a, dove
a=3, possiamo applicare la
Regola di Ruffini
Il polinomio dividendo è già ordinato e completo, quindi passiamo subito a riempire opportunamente la "griglia" di Ruffini e fare i conti secondo l' algoritmo che conosciamo:
Nella riga in basso, nella parte centrale, abbiamo trovato i coefficienti 1, -1, 2 del polinomio quoziente, Q(x), mentre il numero più a destra, 2, è il resto, R, della divisione.
Essendo il resto un polinomio di grado inferiore al grado del polinomio divisore (il quale è di grado 1), esso non può che essere un polinomio di grado zero, e dunque un numero, 2, in questo caso.
In conclusione, possiamo scrivere che il polinomio dividendo è uguale alla somma tra il prodotto del divisore per il quoziente e il resto:
Ex.2
Il secondo e ultimo esercizio di questo tutorial chiede di eseguire questa
divisione tra polinomi:
Come puoi vedere, il polinomio divisore NON è nella forma x+a, e dunque occorre fare delle opportune manipolazioni prima di poter applicare la Regola di Ruffini.
Prima di andare avanti, ti invito a non perderti i miei prossimi nuovi esercizi svolti: iscriviti gratis.
Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.
Se vuoi invece ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.
Bene! Sappiamo che una volta trovati il quoziente, Q(x), e il resto, R, potremo scrivere così:
Semplifichiamo:
In questo modo, possiamo applicare la
Regola di Ruffini
eseguendo la divisione
Questa divisione, eseguita con la regola di Ruffini (il divisore è del tipo x+a), ci darà esattamente il quoziente, Q(x), che stiamo cercando ed un resto, r, che è uguale ad un terzo del resto, R, che stiamo cercando.
Applichiamo dunque l' algoritmo visto precedentemente (il polinomio dividendo è già ordinato e completo):
Abbiamo così trovato i coefficienti del polinomio quoziente e il resto r, che dovrà essere moltiplicato per 3 se vogliamo ottenere il resto R che stiamo cercando.
Ecco il quoziente Q(x) ed il resto R:
In conclusione, possiamo scrivere che il polinomio dividendo è uguale alla somma tra il prodotto del divisore per il quoziente e il resto:
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto:
troverai un' ampia raccolta di esercizi svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
Puoi guardare questa esercitazione nel video qui sotto:



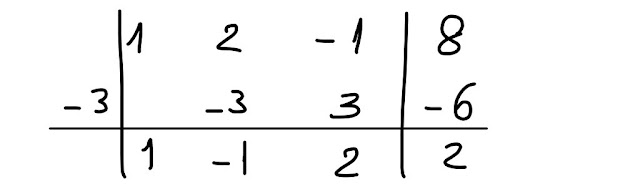









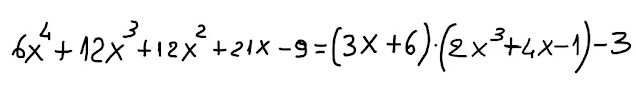










Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)