Disequazioni Goniometriche: Esercizi Svolti

Ultimo Aggiornamento: 10/04/2022

Come si risolvono le disequazioni goniometriche

Ciao! Sono Giuseppe.

Fig. 0

In questo blog, pubblico

esercizi svolti di matematica

per le scuole superiori e l' università.

Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.

In questo tutorial, ti propongo 2 esercizi svolti e commentati.

Ok, se mi segui, sarà tutto più semplice! 😃

Il primo esercizio che svolgerò in questo tutorial 

è il seguente:

Esercizio n. 1

Risolvi la disequazione

[1-sin(x)]⋅[√6-√2 ⋅ cotan(x)] ≤ 0

Svolgimento

[1-sin(x)]⋅[√6-√2 ⋅ cotan(x)] ≤ 0

Studiamo il segno di ciascuno dei due fattori evidenziati in arancione:

I)

1-sin(x) > 0

II)

√6-√2 ⋅ cotan(x) > 0

Si tratta di risolvere due disequazioni (la I e la II) più semplici rispetto alla disequazione assegnata.

Risolviamo la disequazione I):

1-sin(x) > 0

     ↓

sin(x) < 1

Ora, sin(x) è minore di 1

∀ x ≠ π/2 + 2kπ

Ricordiamo che k rappresenta un numero intero relativo qualunque (k ∈ Z)

fig. 1

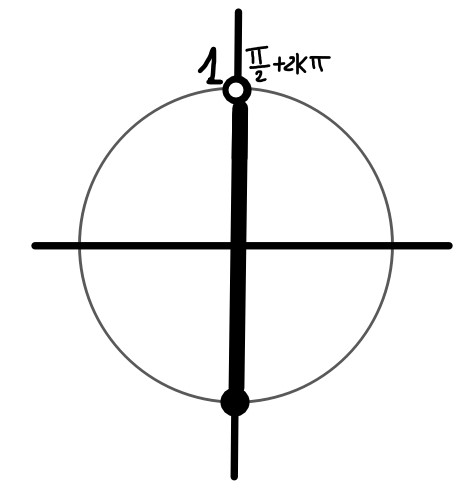
La fig. 1 ci aiuta a vedere che il sin(x) è minore di 1 per ogni (∀) valore della x, tranne l' angolo π/2 e tutti i sui angoli omologhi.

Andiamo avanti, con la disequazione II):

√6-√2 ⋅ cotan(x) > 0

           ↓

√6 > √2 ⋅ cotan(x)

         ↓

√6/√2 > cotan(x)

     ↓

cotan(x) < √3

La domanda è:

per quali valori della x la cotangente è minore della radice quadrata di 3?

Niente panico! Ci viene in aiuto la fig. 2 qui sotto:

fig. 2

π/6 + kπ < x < π + kπ

La fig. 2 ci mostra che per tutti i valori della x compresi tra π/6 e π (arco verde superiore, estremi esclusi), la cotangente è minore della radice quadrata di 3; ma anche per tutti i valori della x compresi tra 7π/6 e 2π (fig. 4 qui sotto: arco verde inferiore, estremi esclusi), la cotangente è minore della radice quadrata di 3❗

E poi, siccome non possiamo trascurare tutti gli angoli omologhi, ecco il perché della scrittura compatta

π/6 + kπ < x < π + kπ

che rappresenta, in pratica, tutte le soluzioni della disequazione II) visualizzabili mediante "rotazioni rigide" dell' arco verde superiore che vedi in fig. 2, sia in senso orario sia in senso antiorario, di angoli che sono multipli di 180⁰ (π).

Dunque, ricapitolando:

I)

1-sin(x) > 0

∀ x ≠ π/2 + 2kπ

fig. 3

II)

√6-√2 ⋅ cotan(x) > 0

per

π/6 + kπ < x < π + kπ

fig. 4

Adesso, mettendo insieme le informazioni sui segni dei due fattori che avevamo individuato subito nel primo membro della disequazione assegnata, si ha la fig. 5 qui sotto, molto utile a concludere questo primo esercizio:

fig. 5

Come puoi vedere in fig. 5, la circonferenza più interna mostra che il primo fattore,

1-sin(x) 

è positivo per ogni valore di

x ≠ π/2 + 2kπ

ed è nullo per 

x=π/2 + 2kπ

La circonferenza più esterna, invece, mostra che il secondo fattore,

√6-√2 ⋅ cotan(x)

è positivo per

π/6 + kπ < x < π + kπ ;

è negativo per 

0 + hπ < x < π/6 + hπ ;

è nullo per

x = π/6 + kπ

E se proprio vogliamo dirla tutta, il secondo fattore non ha senso per

x = kπ

(k ∊ Z)

Dunque, dato che il prodotto dei due fattori individuati nella nostra disequazione assegnata deve essere minore o uguale a zero, gli angoli che risolvono sono negli intervalli (vedi fig. 5) in cui i segni sono discordi, cioè

π + kπ < x ≤ 7π/6 + kπ

insieme con

x=π/2 + 2kπ

Beh, gli archi

7π/6 + kπ

vengono inclusi perché in corrispondenza di questi archi si annulla il secondo fattore e di conseguenza si azzera il prodotto tra i due fattori.

Stesso discorso per gli archi 

x=π/2 + 2kπ

Qui si annulla il primo fattore.

C' è un modo alternativo ed equivalente di scrivere le soluzioni, che è questo:

0 + kπ < x ≤ π/6 + kπ

insieme con l' ormai immancabile 😃

x=π/2 + 2kπ

Prima di andare avanti col secondo e ultimo esercizio, ci tengo a dirti che puoi imparare di più e finalmente puoi iniziare a migliorare i tuoi voti in matematica attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è

Matematica Quinquennio

Se vuoi imparare a risolvere gli esercizi di matematica con più serenità e abilità, allora è arrivato il momento di iniziare il tuo percorso gratuito; fai click sul link qui sotto:

iscriviti gratis qui.

Bene, torniamo all' esercizio!

Disequazioni Goniometriche: come si risolvono

Esercizio n. 2

Risolvi la disequazione

1-2sin²(x) ≥ 0

Svolgimento

Andiamo a scomodare una variabile ausiliaria, che indicheremo con la lettera z, e poniamo

sin(x)=z

Così facendo, possiamo riscrivere la disequazione in questo modo:

1-2z² ≥ 0

Per risolvere questa disequazione, che presenta l' incognita z , facciamo un disegnino:

sul piano cartesiano "grafichiamo" la funzione

y = 1-2z² (primo membro dell' ultima disequazione che ho scritto)

e disegniamo anche 

y = 0 (secondo membro della stessa disequazione)

fig. 6

La fig. 6 ci fa vedere la parabola di colore blu,

y = 1-2z² ,

che interseca in due punti distinti l' asse delle ascisse,

y = 0 

Siccome la disequazione è

1-2z² ≥ 0 ,

dobbiamo vedere (fig. 6) per quali valori della z il grafico della parabola sta sopra (>) o interseca (=) l' asse orizzontale delle ascisse .

Per trovare i punti di intersezione tra la parabola e l' asse delle ascisse basta risolvere un semplice sistemino (non sto a scriverlo), che ci porta a dover risolvere l' equazione

1-2z² = 0

Risolvendo questa equazione, si ottengono due valori reali distinti (riportati in fig. 6):

z₁=-√2/2

z₂=√2/2

Questi due valori sono le ascisse dei due punti di intersezione tra la parabola e l' asse z .

Qual era la domanda?

Dove la parabola sta sopra (>) o interseca (=) l' asse orizzontale delle ascisse ?

La fig. 6 ci dice che le soluzioni della disequazione sono date dai valori della z compresi tra -√2/2 e √2/2, estremi inclusi, e dunque scriviamo:

-√2/2 ≤ z ≤ √2/2

Ma che cosa rappresenta z ?

Te lo ricordi? Lo abbiamo scritto prima, proprio all' inizio dello svolgimento di questo secondo esercizio.

z=sin(x)

Dunque

-√2/2 ≤ z ≤ √2/2

diventa

-√2/2 ≤ sin(x) ≤ √2/2

Alla fine, il nostro problemino è capire per quali valori della x il seno (sin) è compreso tra

-√2/2 e √2/2 (estremi inclusi).

Bene, ricorriamo ad un utile disegno:

fig. 7

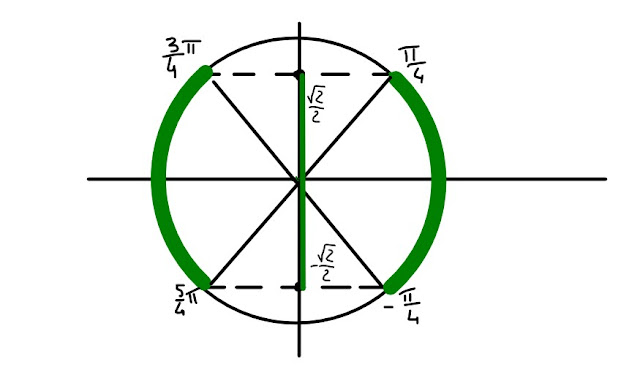
La fig. 7 ci dice che gli angoli che hanno il seno compreso tra

-√2/2 e √2/2, estremi inclusi, sono quelli compresi tra

 

-π/4 e π/4 (estremi inclusi)

oppure tra

3π/4 e 5π/4 (estremi inclusi)

Considerando, poi, tutti gli angoli omologhi, scriviamo le soluzioni in questo modo:

-π/4 + 2kπ ≤ x ≤ π/4 + 2kπ

(k ∈ Z)

oppure

3π/4 + 2hπ ≤ x ≤ 5π/4 + 2hπ

(h ∈ Z)

Ultima domanda:

esiste una scrittura più compatta delle soluzioni della disequazione?

Se sì, quale potrebbe essere una scrittura più compatta ed equivalente a quella che ho scritto io?

Puoi rispondere nella sezione dedicata ai commenti.

Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e scopri nel link qui sotto come puoi migliorare i tuoi voti in matematica:

troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.

Alla prossima lezione. Ciao, ti aspetto!

Puoi seguire questa esercitazione guardando il video qui sotto: