come si trovano i punti di cuspide di una funzione?
Un' altra domanda è:
se ci sono,
In questo blog pubblico
esercizi svolti di matematica
per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi.
Esercizio n. 1
Trova i punti di minimo e massimo relativo della funzione
y=3+|x²-x| ,
facendo distinzione tra
punti stazionari
e
punti angolosi
Svolgimento
Possiamo sciogliere il valore assoluto della funzione assegnata come segue:
Ciò che ho scritto in fig. 1 deriva dall' applicazione della definizione di valore assoluto, che puoi trovare qui.
Come puoi vedere nella fig. 1, la nostra funzione assegnata, quella che presenta il valore assoluto, diventa una funzione a pezzi:
y=x²-x+3
laddove la x soddisfa la disequazione
x²-x≥0, cioè per
x≤0 o x≥1 (osserva la fig. 3 qui sotto)
oppure, secondo pezzo,
y=-x²+x+3
laddove la x soddisfa la disequazione
x²-x<0, cioè per
0<x<1 (osserva la fig. 3 qui sotto)
Dunque possiamo riscrivere la nostra funzione assegnata, dopo aver sciolto il valore assoluto, in questo modo:
Nella fig. 3 qui sotto, puoi capire meglio, per via grafica, il perché delle restrizioni sulla x scritte in fig. 2
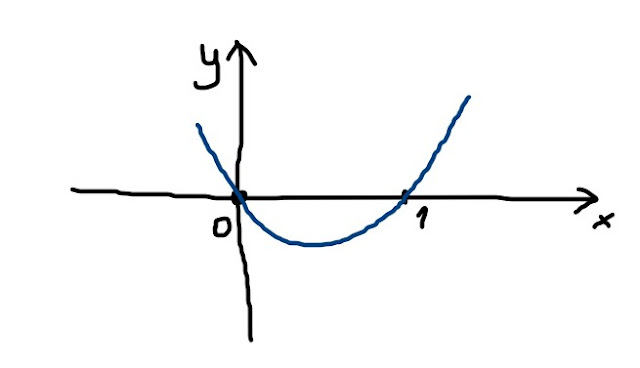
Graficando la funzione (fig. 3)
y=x²-x ,
possiamo vedere in quali intervalli della x il grafico della parabola sta sopra o sotto l'asse delle ascisse:
Ecco, puoi vedere che la parabola
y=x²-x
sta sopra o interseca ( ≥ 0 ) l'asse delle ascisse per
x≤0 o x≥1
Inoltre, la parabola sta sotto ( < 0 ) l'asse delle ascisse per
0<x<1
Dopo questa spiegazione, facciamo vedere nella fig. 4 qui sotto gli intervalli in cui giacciono i pezzi del grafico della funzione assegnata:
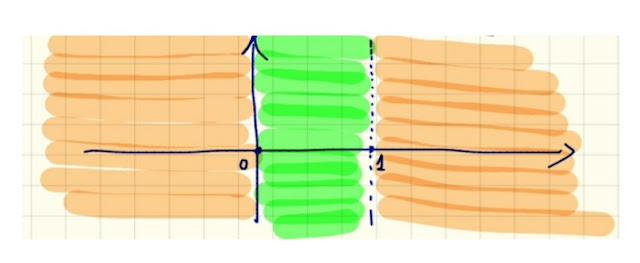 |
| fig. 4 |
Come puoi vedere in fig. 4, nelle porzioni del piano cartesiano evidenziate in arancione, corrispondenti agli intervalli
x≤0 o x≥1 ,
si sviluppa il grafico della funzione
y=x²-x+3
Invece, nella porzione del piano cartesiano evidenziata in verde, corrispondente all' intervallo
0<x<1 ,
si sviluppa il grafico della funzione
y=-x²+x+3
Bene! Adesso, visti gli scopi di questa esercitazione, andiamo a fare un po' di "analisi al microscopio" 🔬 😎
Calcoliamo il limite per x che tende a zero della funzione assegnata e poi calcoliamo il valore che la funzione stessa assume per x=0.
Se il limite per x che tende a zero della funzione assegnata è uguale al valore che la funzione stessa assume in x=0, allora la funzione del nostro primo esercizio è continua in x=0.
Facciamo un po' di conticini importanti:
Nella fig. 5, ho calcolato due limiti:
uno scritto a sinistra, l'altro scritto a destra.
Prendiamo adesso in considerazione quello scritto a sinistra:
il limite della funzione per x che tende a zero, da sinistra (0⁻), vale 3, per eccesso (3⁺). Puoi notare che ho calcolato il limite per x che tende a 0⁻ della funzione
y=x²-x+3 ,
visto che questa si riferisce all' intervallo
x≤0 o x≥1
↑
0⁻ significa zero da sinistra (poco meno di zero, per intenderci)
Prendiamo adesso in considerazione quello scritto a destra:
il limite della funzione per x che tende a zero, da destra (0⁺), vale anch' esso 3, per eccesso (3⁺). Puoi notare che ho calcolato il limite per x che tende a 0⁺ della funzione
y=-x²+x+3 ,
visto che questa si riferisce all' intervallo
0<x<1
Calcoliamo adesso il valore della funzione assegnata in x=0:
f(x)=3+|x²-x|
f(0)=3+|0²-0|=3
Ecco, siccome il limite per x che tende a zero della funzione assegnata è uguale al valore che la funzione stessa assume per x=0, essa è continua in x=0
Domanda:
la nostra funzione assegnata è derivabile in x=0 ❓
 |
| fig. 6 |
Calcoliamo i due limiti che vedi nella fig. 6, limiti della derivata prima (limite sinistro e limite destro):
Poiché il limite scritto a sinistra nella fig. 6 è per x che tende a 0⁻ (a zero da sinistra), la derivata prima deve essere la derivata della funzione che si riferisce all' intervallo
x≤0 o x≥1
Si tratta dunque di derivare la funzione
y=x²-x+3 ,
e otteniamo
y'= 2x-1 (vedi il limite scritto a sinistra nella fig. 7)
Poiché il limite scritto a destra nella fig. 6 è per x che tende a 0⁺ (a zero da destra), la derivata prima deve essere la derivata della funzione che si riferisce all' intervallo
0<x<1
Si tratta dunque di derivare la funzione
y=-x²+x+3 ,
e otteniamo
y'=-2x+1 (vedi il limite scritto a destra nella fig. 7)
La domanda era:
la nostra funzione assegnata è derivabile in x=0 ❓
La risposta è no, perché il limite della derivata prima per x che tende a zero da sinistra e il limite della derivata prima per x che tende a zero da destra sono diversi e valgono rispettivamente -1 e 1.
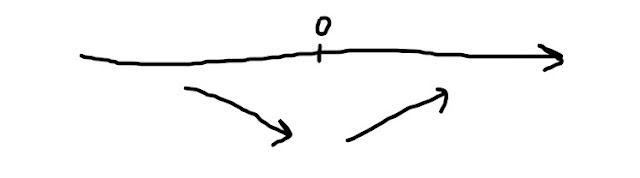
Ora, siccome la derivata prima, per x che tende a zero da sinistra, tende a -1, e dato che la derivata prima, per x che tende a zero da destra, tende a 1, si ha che (fig. 8 qui sotto) la funzione decresce in un intorno sinistro di zero e cresce in un intorno destro di zero
In x=0 abbiamo dunque un minimo relativo, che è anche punto angoloso.
Vediamo adesso come vanno le cose in x=1.
Calcoliamo il limite per x che tende a 1 della funzione assegnata e poi calcoliamo il valore che la funzione stessa assume per x=1.
Se il limite per x che tende a 1 della funzione assegnata è uguale al valore che la funzione stessa assume in x=1, allora la funzione del nostro primo esercizio è continua in x=1.
Facciamo anche qui un po' di conticini coi limiti:
Da notare che la funzione di cui calcolo il limite per x che tende a 1 da destra è quel "pezzo" relativo all' intervallo
x≤0 o x≥1 ,
↑
1⁺ significa 1 da destra (poco più di 1)
mentre la funzione di cui calcolo il limite per x che tende a 1 da sinistra è quel "pezzo" relativo all' intervallo
0<x<1
La fig. 9 ci dice che il limite della funzione del nostro esercizio per x che tende a 1 vale 3.
Vediamo che valore assume questa funzione assegnata in x=1:
f(x)=3+|x²-x|
f(1)=3+|1²-1|=3
Ecco, siccome il limite per x che tende a 1 della funzione assegnata è uguale al valore che la funzione stessa assume per x=1, essa è continua in x=1
Domanda, come prima:
la nostra funzione assegnata è derivabile in x=1 ❓
 |
| fig. 10 |
Calcoliamo i due limiti che vedi nella fig. 10, limiti della derivata prima (limite per x che tende a 1 da destra e limite per x che tende a 1 da sinistra):
 |
| fig. 11 |
Siccome il limite della derivata prima per x che tende a 1 da destra e il limite della derivata prima per x che tende a 1 da sinistra sono diversi e valgono rispettivamente 1 e -1, la nostra funzione assegnata non è derivabile in x=1.
Come prima, ragioniamo così:
siccome la derivata, per x che tende a 1 da destra, tende a 1, e dato che la derivata prima, per x che tende a 1 da sinistra, tende a -1, si ha che (fig. 12 qui sotto) la funzione decresce in un intorno sinistro di 1 e cresce in un intorno destro di 1
 |
| fig. 12 |
Anche in x=1 abbiamo un minimo relativo, che è pure un punto angoloso.
Andiamo avanti, ripartendo dal primo pezzo della funzione assegnata e cerchiamo qualche punto stazionario (se esiste):
Sappiamo la derivata prima:
y'=2x-1
Cerchiamo la soluzione dell' equazione
y'=0
2x-1=0 → x=1/2
Dato che
1/2 ∉ ]-∞,0]∪[1,+∞[
non ha senso andare avanti.
Passiamo al secondo pezzo della funzione assegnata e cerchiamo qui qualche punto stazionario (se esiste):
 |
| fig. 14 |
Sappiamo anche la derivata prima di questo secondo pezzo, quello che si riferisce all' intervallo compreso tra 0 e 1, estremi esclusi:
y'=-2x+1
Cerchiamo la soluzione dell' equazione
y'=0
-2x+1=0 → x=1/2
Dato che
1/2 ∊ ]0,1[
andiamo a vedere il valore
della derivata seconda in
x=1/2
Siccome
y''=-2 ,
banalmente, la derivata seconda in
x=1/2
vale -2 (negativa), e quindi, essendo la concavità rivolta verso il basso, in
x=1/2
abbiamo un punto di massimo relativo, che è anche un punto stazionario, visto che in esso la derivata prima si annulla:
y'(1/2)=0
E ora, per soddisfare la curiosità di vedere come si disegna questa funzione, sfruttiamo alcune semplici
trasformazioni geometriche
Sappiamo che vogliamo disegnare la funzione assegnata
y=3+|x²-x|
Prima di tutto, disegno la funzione
a) y=x²-x ;
poi disegno la funzione
b) y=|x²-x| ;
e per finire disegno la nostra funzione assegnata
c) y=3+|x²-x|
Se vuoi ripassare le
trasformazioni geometriche applicate ai grafici delle funzioni,
allora vai qui.
Iniziamo a disegnare i grafici, dal più semplice al più complesso:
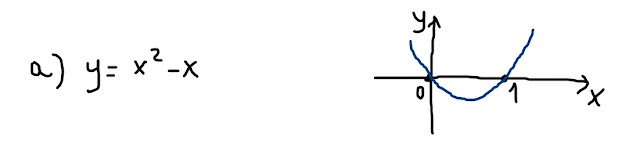 |
| fig. 15 |
Nella fig. 15 ho disegnato la funzione a) che mi è stata "suggerita" dall'argomento del valore assoluto presente nella funzione assegnata.
Nella fig. 16 ho disegnato la funzione b) partendo dalla funzione a) sulla quale ha agito il valore assoluto (come puoi vedere, viene "simmetrizzata" rispetto all'asse x la porzione di grafico che stava sotto l'asse orizzontale, per effetto del valore assoluto).
Nella fig. 17 ho disegnato la funzione c), cioè la funzione assegnata, partendo dalla funzione b) sulla quale ha agito una traslazione verticale verso l'alto (+3)
Ne
N
N
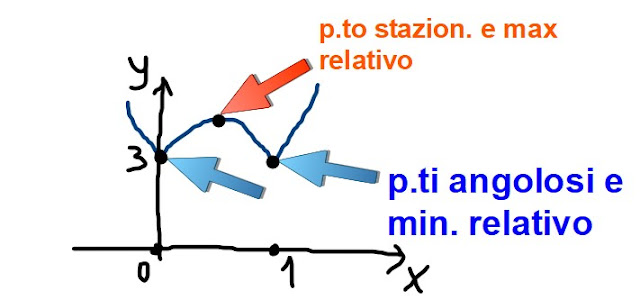
Per finire col primo esercizio, nella fig. 18 sono indicati i due punti angolosi, che sono anche punti di minimo relativo, e il punto stazionario, che è anche punto di massimo relativo.
Prima di andare avanti, ci tengo a dirti che puoi imparare di più e finalmente puoi iniziare a migliorare i tuoi voti in matematica attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è
Matematica Quinquennio
Se vuoi imparare a risolvere gli esercizi di matematica con più serenità e abilità, allora è arrivato il momento di iniziare il tuo percorso gratuito; fai click sul link qui sotto:
Bene, andiamo al secondo e ultimo esercizio di questa esercitazione!
Ecco il secondo esercizio che svolgerò in questo tutorial:
Esercizio n. 2
 |
| fig. 19 |
Di questa funzione trova i punti di massimo e di minimo relativi, specificando se si tratta di cuspidi.
Svolgimento
Il dominio coincide con tutto l'insieme dei numeri reali:
D=R
Perché?
Perché ha senso la radice quinta del quadrato di x qualunque sia il valore di x.
Calcoliamo la derivata prima, y', di questa funzione assegnata:
 |
| fig. 20 |
Come vedi in fig. 20, ho riscritto la funzione da derivare come potenza con esponente razionale.
Andiamo avanti col calcolo della derivata prima, che poi poniamo uguale a zero:
Beh, la derivata prima non si annulla mai!
Quindi non ci sono punti stazionari.
Inoltre la funzione in x=0 non è derivabile perché la derivata prima in x=0 non ha senso, non è definita, visto che x=0 annulla il denominatore che compare nella derivata (fig. 21).
Però in x=0 la funzione è continua!
Vediamo perché:
Come puoi vedere, il limite della funzione assegnata, per x che tende a zero, vale zero, per eccesso (0⁺), e la funzione in x=0 vale zero. Quindi la funzione in x=0 è continua.
Abbiamo detto che la derivata prima non ha senso in x=0. Andiamo a vedere di cosa si tratta.
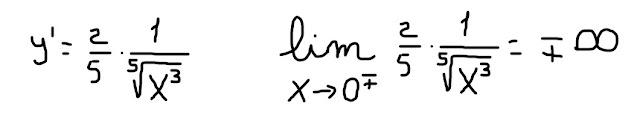 |
| fig. 23 |
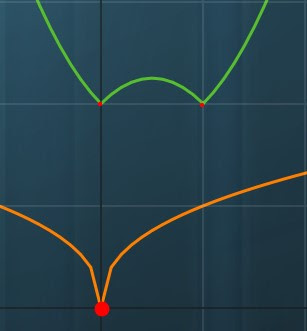
Siccome il limite della derivata prima per x che tende a zero da sinistra (0⁻) vale meno infinito e il limite della derivata prima per x che tende a zero da destra (0⁺) vale più infinito, in x=0 abbiamo un punto di cuspide, con la punta della "freccia" verso il basso: ⋎
Possiamo concludere che in x=0, oltre ad avere un punto di cuspide (⋎), abbiamo un punto di minimo relativo, come si vede anche in fig. 24.
 |
| fig. 24 |
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e scopri nel link qui sotto come puoi migliorare i tuoi voti in matematica:
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!









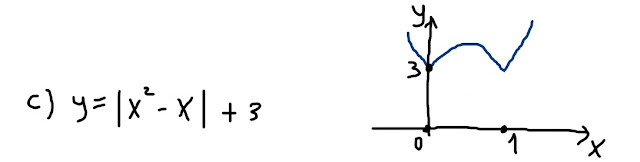












Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)