In questa esercitazione, vedremo lo svolgimento, nei dettagli, di 3 esercizi di matematica per le Superiori; in particolare affronteremo 2 equazioni e 1 disequazione con valore assoluto.
Imparerai a risolvere, col giusto metodo, equazioni e disequazioni in cui sono presenti queste "cose strane" che si chiamano valori assoluti, o moduli, e che fanno sembrare orribili le dis-equazioni. 😲
Tranquilli, se mi seguite, sarà tutto più semplice! 😃
Imparerai a risolvere, col giusto metodo, equazioni e disequazioni in cui sono presenti queste "cose strane" che si chiamano valori assoluti, o moduli, e che fanno sembrare orribili le dis-equazioni. 😲
Tranquilli, se mi seguite, sarà tutto più semplice! 😃
Se vuoi questa lezione in PDF stampabile, sempre a portata di mano, consultabile tutte le volte che vuoi, allora fai click sul pulsante qui sotto e scopri come ottenerla:
👇
👆
Risolvere questa equazione:
2•|3+x| + 3x = |x-1| - 4x

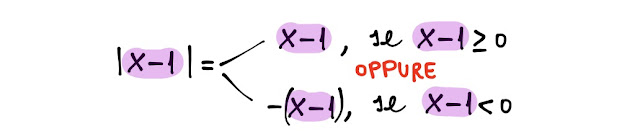
Prima di andare avanti, ti invito a non perderti i miei prossimi nuovi esercizi svolti: iscriviti gratis.
Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.
Se vuoi invece ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.
Torniamo al nostro 1° esercizio.
Se hai dubbi, osservazioni, non esitare a lasciare un commento qui sotto ✍✍✍


Perché c' è la faccetta triste?
Perché 7/6 non è minore di -3
Esercizio 1 di 3
Come si risolve un' equazione col valore assoluto
Risolvere questa equazione:
2•|3+x| + 3x = |x-1| - 4x
Ricordiamo la definizione di valore
assoluto e poi facciamo un esempio:
Fig. 1.1
Questa scrittura che vedi nella
figura 1.1 significa che il valore
assoluto di a (argomento) è uguale
ad a, se a è maggiore o uguale a
zero,
oppure
il valore assoluto di a (argomento) è uguale a - a, se a è minore di zero.
Proviamo a fare un primo esempio
Proviamo a fare un primo esempio
attribuendo ad a il valore -7.
Calcoliamo, seguendo la definizione
Calcoliamo, seguendo la definizione
di fig. 1.1, il valore assoluto di -7:
| -7 | = -( -7) = 7, perchè -7 < 0
E quanto vale | 7 | ?
L' argomento, questa volta, è 7 ( ≥ 0 ), quindi | 7 | = 7
| -7 | = -( -7) = 7, perchè -7 < 0
E quanto vale | 7 | ?
L' argomento, questa volta, è 7 ( ≥ 0 ), quindi | 7 | = 7
Esempio:
Fig. 1.2
Nella fig. 1.2 non abbiamo fatto altro
che applicare la definizione di
valore assoluto (modulo), che vedi
nella figura 1.1, per "sciogliere",
diciamo così, il valore assoluto di
x - 1 .
In pratica, possiamo “sciogliere”
il valore assoluto di x - 1,
scrivendo che
|x - 1|=x - 1, se x - 1 ≥ 0,
cioè se x ≥ 1
oppure
|x - 1|= - (x - 1) = -x + 1,
se x - 1 < 0,
cioè se x < 1
Non spaventatevi, perchè faremo
degli esercizi più sostanziosi,
e così capiremo meglio.
Studiamo il segno di ogni
espressione “ingabbiata” nel
valore assoluto ( | … | )
Prima di andare avanti, ti invito a non perderti i miei prossimi nuovi esercizi svolti: iscriviti gratis.
Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.
Se vuoi invece ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.
Torniamo al nostro 1° esercizio.
Ci conviene studiare il segno di ogni
espressione “ingabbiata” nel
valore assoluto ( | … | ).
Riprendiamo la nostra equazione:
2•|3+x| + 3x = |x-1| - 4x
Le espressioni ingabbiate nel valore
Riprendiamo la nostra equazione:
2•|3+x| + 3x = |x-1| - 4x
Le espressioni ingabbiate nel valore
assoluto sono 3+x e x-1, di cui
studieremo il segno.
3+x > 0 ⟶ x > -3
x-1 > 0 ⟶ x > 1
Facciamo il grafico con le linee dei
3+x > 0 ⟶ x > -3
x-1 > 0 ⟶ x > 1
Facciamo il grafico con le linee dei
segni:
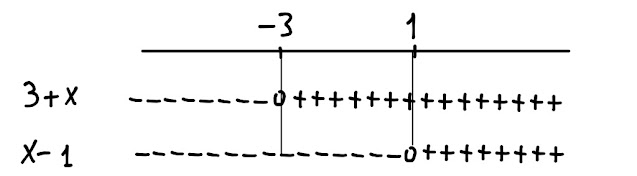
L' argomento del primo valore
Fig 1.3
L' argomento del primo valore
assoluto, 3+x, è positivo per
x > -3, è negativo per x < -3
e nullo per x = -3.
L' argomento del secondo
L' argomento del secondo
valore assoluto, x-1, è
positivo per x > 1, è negativo
per x < 1 e nullo per x = 1.
Stando alla definizione di figura 1.1,
per x < 1 e nullo per x = 1.
Stando alla definizione di figura 1.1,
possiamo "sciogliere" i valori
assoluti della nostra equazione
assegnata in questo modo:
eq.1:
eq.1:
2•[-(3+x)] + 3x = -(x-1) - 4x
ed x < -3
oppure
eq.2:
oppure
eq.2:
2•(3+x) + 3x = -(x-1) - 4x
e -3 ≤ x < 1
oppure
eq.3:
oppure
eq.3:
2•(3+x) + 3x = x-1 - 4x
ed x ≥ 1
Risolviamo queste tre equazioni,
Risolviamo queste tre equazioni,
tenendo conto delle loro rispettive
restrizioni sulla x.
Se hai dubbi, osservazioni, non esitare a lasciare un commento qui sotto ✍✍✍
Perché c' è la faccetta triste?
Perché 7/6 non è minore di -3
(7/6 non è accettabile!)

Qui la faccina è allegra perchè -1/2 è compreso tra -3 e 1, quindi x = -1/2 è accettabile.


Anche -7/8 non si può accettare. Perchè?
Per concludere il discorso sull' equazione del 1° esercizio, la sua soluzione è x = -1/2.
Avanti con l'
Se hai un' azienda o conosci qualcuno che la possiede, potrebbe esserti molto utile Amazon Business. L' iscrizione è gratuita! ⚙🔝
Risolviamo questa seconda equazione:


Qui la faccina è allegra perchè -1/2 è compreso tra -3 e 1, quindi x = -1/2 è accettabile.
Anche -7/8 non si può accettare. Perchè?
Per concludere il discorso sull' equazione del 1° esercizio, la sua soluzione è x = -1/2.
Avanti con l'
Esercizio 2 di 3
Come si risolve un' equazione col valore assoluto
Se hai un' azienda o conosci qualcuno che la possiede, potrebbe esserti molto utile Amazon Business. L' iscrizione è gratuita! ⚙🔝
Risolviamo questa seconda equazione:
Beh, diciamo subito che x ≠ 1, perché
altrimenti si azzera il denominatore,
|1-x|.
Studiamo il segno di ogni
Studiamo il segno di ogni
espressione “ingabbiata” nel
valore assoluto.
x > 0
2 + x > 0 ⟶ x > -2
1 - x > 0 ⟶ x < 1
Facciamo il grafico con le linee dei
x > 0
2 + x > 0 ⟶ x > -2
1 - x > 0 ⟶ x < 1
Facciamo il grafico con le linee dei
segni:
Hai bisogno di una buona Calcolatrice Scientifica?
Scopri qual è quella più diffusa tra i miei studenti, in questo momento. 😊
Stando alla definizione di figura 1.1,
Scopri qual è quella più diffusa tra i miei studenti, in questo momento. 😊
Stando alla definizione di figura 1.1,
possiamo "sciogliere" i valori assoluti
della nostra equazione assegnata in
questo modo:

oppure
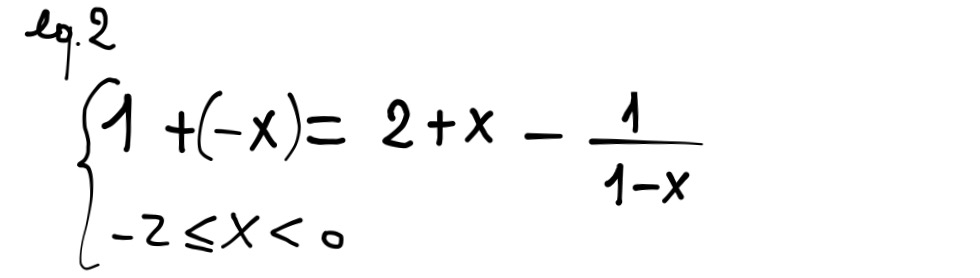
oppure

oppure
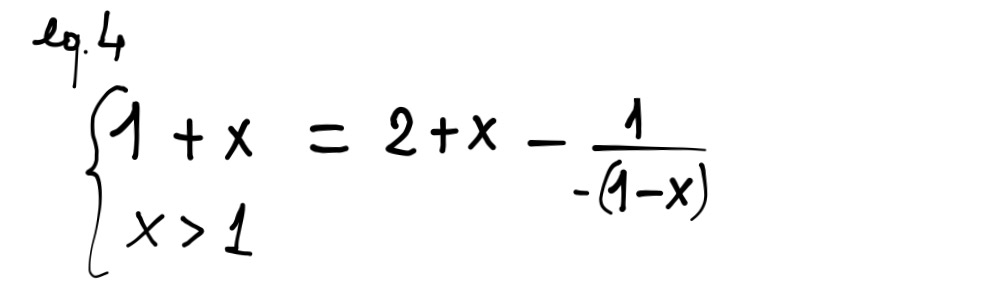
Risolviamo queste quattro equazioni,
oppure
oppure
oppure
Risolviamo queste quattro equazioni,
tenendo conto delle loro rispettive
restrizioni sulla x.


Andiamo avanti:

La faccina è triste perchè 4/3 NON è minore di -2. La condizione, qui, è x < -2
4/3 NON è accettabile!
Ancora avanti:



Perché 0 e 1/2, qui, sono entrambi inaccettabili?
Perché non soddisfano la condizione -2 ≤ x < 0
Prima di andare avanti con la terza equazione e le sue restrizioni sulla x, ti chiedo se stai cercando una buona e poco costosa calcolatrice grafica senza calcolo simbolico.
Guarda questa.


Come vedi, adesso siamo autorizzati ad accettare x=0 come soluzione, perchè soddisfa la condizione
0 ≤ x < 1
Procediamo verso la quarta equazione.
Dai anche un' occhiata alle mie raccolte di esercizi che ho ampiamente svolto e commentato.
In questo momento sono pure disponibili questi miei 3 ebooks:
- Monomi (20 esercizi svolti e commentati);
- Grafici con le Trasformazioni Geometriche (13 esercizi svolti e commentati);
- Principio di Induzione ( 7 esercizi svolti e commentati ).

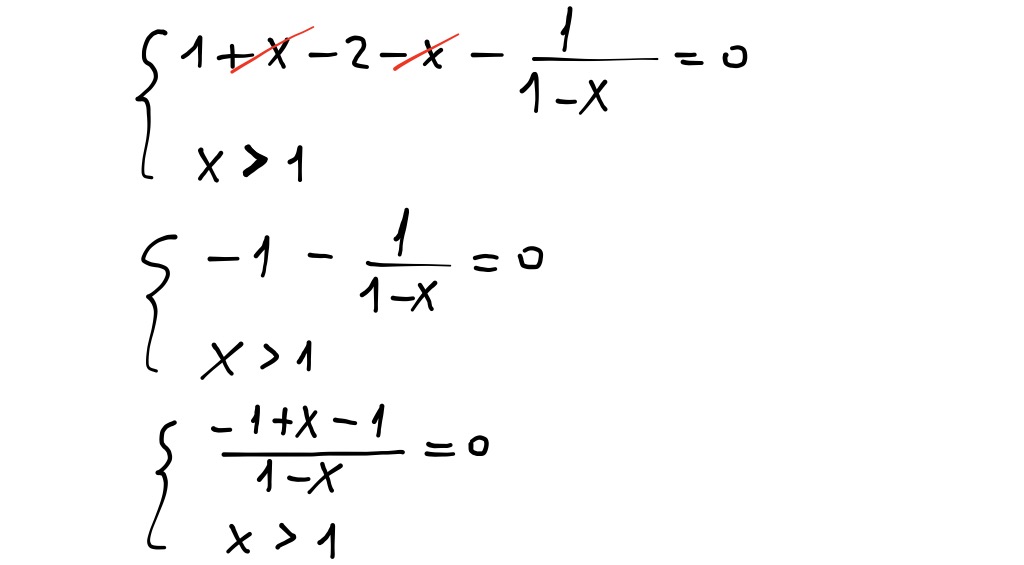

Anche 2 è accettabile perché
Andiamo avanti:
La faccina è triste perchè 4/3 NON è minore di -2. La condizione, qui, è x < -2
4/3 NON è accettabile!
Ancora avanti:
Perché 0 e 1/2, qui, sono entrambi inaccettabili?
Perché non soddisfano la condizione -2 ≤ x < 0
Prima di andare avanti con la terza equazione e le sue restrizioni sulla x, ti chiedo se stai cercando una buona e poco costosa calcolatrice grafica senza calcolo simbolico.
Guarda questa.
Come vedi, adesso siamo autorizzati ad accettare x=0 come soluzione, perchè soddisfa la condizione
0 ≤ x < 1
Procediamo verso la quarta equazione.
Dai anche un' occhiata alle mie raccolte di esercizi che ho ampiamente svolto e commentato.
In questo momento sono pure disponibili questi miei 3 ebooks:
- Monomi (20 esercizi svolti e commentati);
- Grafici con le Trasformazioni Geometriche (13 esercizi svolti e commentati);
- Principio di Induzione ( 7 esercizi svolti e commentati ).
Anche 2 è accettabile perché
2 > 1
Concludiamo dicendo che l' equazione coi valori assoluti del nostro secondo esercizio ha le seguenti soluzioni:
Tra un po' affronteremo una disequazione coi valori assoluti.
Per non perderti i miei prossimi nuovi esercizi svolti, iscriviti gratis.
Risolviamo questa disequazione:
Poniamo queste espressioni > 0:
2(x - 1) > 0
x - 16 > 0
Sono due semplici disequazioni di 1° grado, che risolviamo:
2(x - 1) > 0 ⟶ x > 1
x - 16 > 0 ⟶ x > 16
Visualizziamo queste informazioni

Per x < 1, entrambi gli argomenti sono negativi, quindi riscriviamo la disequazione assegnata così:
-2(x - 1) < -( x - 16 ) + 2x
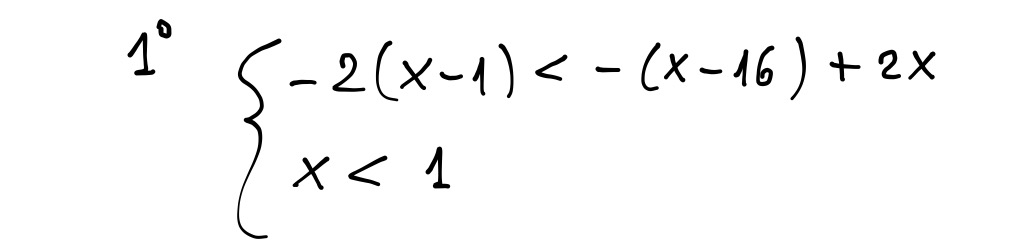

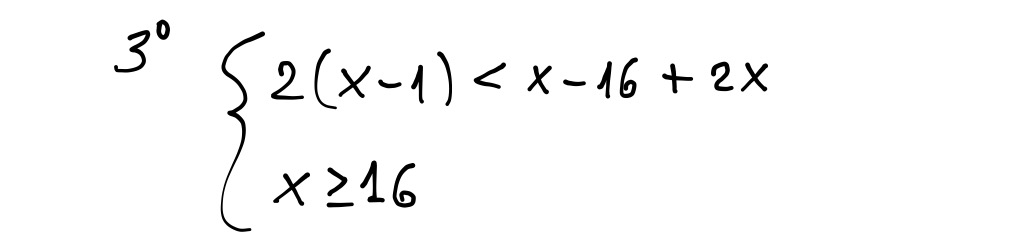
Cominciamo a risolvere il 1° sistema.


Se hai dubbi, osservazioni, o qualche richiesta di chiarimenti, fammi sapere nei commenti; proverò a risponderti compatibilmente con tutti gli altri miei impegni. 😉
E ora visualizziamo con un disegno queste ultime informazioni che si riferiscono alla x, per vedere se ci sono intervalli in cui sono soddisfatte entrambe le disequazioni di questo 1° sistema.

Ripassa un po' come si risolvono i sistemi di disequazioni (puoi andare direttamente al paragrafo 6, che si trova in fondo all' esercitazione).

Visualizziamo, come al solito, queste ultime informazioni relative alla x:

Domanda: in quale intervallo è risolto questo 2° sistema?
Risposta: 1 ≤ x < 16

Disegniamo le nostre utilissime linee continue/discontinue per vedere bene queste ultime informazioni relative alla x:

Bene, il nostro 3° sistema è risolto nell' intervallo
x ≥ 16
Non è ancora finita!
Dobbiamo fare l' unione ( ⋃ ) tra le tre "soluzioni":
-14/3 < x < 1 ⋃ 1 ≤ x < 16 ⋃

Se ora li uniamo, otteniamo:

Questo è l' intervallo risultante e rappresenta le soluzioni della disequazione del nostro terzo e ultimo esercizio di questa esercitazione.
Come possiamo scrivere queste soluzioni con un linguaggio più formale?
Vediamolo!
Aiutaci, con una donazione, a realizzare altre esercitazioni gratuite come questa, che, come puoi immaginare, richiede molto impegno e attenzione.
Inoltre, puoi condividere questa lezione, e ti invito a iscriverti, se non lo hai ancora fatto.

Concludiamo dicendo che l' equazione coi valori assoluti del nostro secondo esercizio ha le seguenti soluzioni:
x = 0 , x = 2
Tra un po' affronteremo una disequazione coi valori assoluti.
Per non perderti i miei prossimi nuovi esercizi svolti, iscriviti gratis.
Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.
Se vuoi ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.
Esercizio 3 di 3
Come si risolve una disequazione col valore assoluto
Risolviamo questa disequazione:
| 2(x - 1) | < | x - 16 | + 2x
Studiamo il segno di ogni
espressione che troviamo nel
valore assoluto.
Poniamo queste espressioni > 0:
2(x - 1) > 0
x - 16 > 0
Sono due semplici disequazioni di 1° grado, che risolviamo:
2(x - 1) > 0 ⟶ x > 1
x - 16 > 0 ⟶ x > 16
Visualizziamo queste informazioni
disegnando le linee dei segni.
Fai un salto su Amazon, dove puoi trovare veramente di tutto. Fai click qui sotto:
Sapendo dove gli argomenti dei valori assoluti sono positivi o nulli e dove invece sono negativi, ricordando la definizione vista in fig. 1.1, andiamo a "sciogliere" la nostra disequazione assegnata.
Per x < 1, entrambi gli argomenti sono negativi, quindi riscriviamo la disequazione assegnata così:
-2(x - 1) < -( x - 16 ) + 2x
Per 1 ≤ x < 16, il 1° argomento è positivo o nullo e il 2° argomento è negativo, quindi riscriviamo la disequazione assegnata così:
2(x - 1) < - (x - 16) + 2x
Per x ≥ 16, entrambi gli argomenti sono positivi o nulli, quindi riscriviamo la disequazione assegnata così:
2(x - 1) < - (x - 16) + 2x
Per x ≥ 16, entrambi gli argomenti sono positivi o nulli, quindi riscriviamo la disequazione assegnata così:
2(x - 1) < x - 16 + 2x
Dunque dobbiamo risolvere, in pratica, questi tre sistemi, e poi faremo l' unione tra le soluzioni che avremo trovato:
Cominciamo a risolvere il 1° sistema.
Se stai cercando anche libri scolastici, puoi trovarli su Amazon. Fai click qui sotto:
Se hai dubbi, osservazioni, o qualche richiesta di chiarimenti, fammi sapere nei commenti; proverò a risponderti compatibilmente con tutti gli altri miei impegni. 😉
E ora visualizziamo con un disegno queste ultime informazioni che si riferiscono alla x, per vedere se ci sono intervalli in cui sono soddisfatte entrambe le disequazioni di questo 1° sistema.
Ripassa un po' come si risolvono i sistemi di disequazioni (puoi andare direttamente al paragrafo 6, che si trova in fondo all' esercitazione).
Come puoi vedere, le due disequazioni del sistema in esame sono soddisfatte nell' intervallo
-14/3 < x < 1 (estremi esclusi)
Risolviamo il 2° sistema.
-14/3 < x < 1 (estremi esclusi)
Risolviamo il 2° sistema.
Qui trovi tantissime altre idee per il tuo Shopping.
Visualizziamo, come al solito, queste ultime informazioni relative alla x:
Domanda: in quale intervallo è risolto questo 2° sistema?
Risposta: 1 ≤ x < 16
Risolviamo il 3° sistema:
Disegniamo le nostre utilissime linee continue/discontinue per vedere bene queste ultime informazioni relative alla x:
Bene, il nostro 3° sistema è risolto nell' intervallo
x ≥ 16
Non è ancora finita!
Dobbiamo fare l' unione ( ⋃ ) tra le tre "soluzioni":
-14/3 < x < 1 ⋃ 1 ≤ x < 16 ⋃
⋃ x ≥ 16
Rappresentiamo con un disegno colorato questi tre intervalli, che poi uniremo.
Sarà interessante "vedere" l' intervallo risultante.
Rappresentiamo con un disegno colorato questi tre intervalli, che poi uniremo.
Sarà interessante "vedere" l' intervallo risultante.
Seguimi sui tuoi Social preferiti; ci vediamo anche lì, ti aspetto! 😊
Se ora li uniamo, otteniamo:
Questo è l' intervallo risultante e rappresenta le soluzioni della disequazione del nostro terzo e ultimo esercizio di questa esercitazione.
Come possiamo scrivere queste soluzioni con un linguaggio più formale?
Vediamolo!
Aiutaci, con una donazione, a realizzare altre esercitazioni gratuite come questa, che, come puoi immaginare, richiede molto impegno e attenzione.
Inoltre, puoi condividere questa lezione, e ti invito a iscriverti, se non lo hai ancora fatto.
Le soluzioni sono:
Ciao, a presto!
S = { x ∈ R | x > -14/3 }
Ciao, a presto!
Puoi guardare questa esercitazione nel video qui sotto:











Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)