 |
| Fig. 1 |
In questa esercitazione vedremo
In questo blog pubblico
esercizi svolti di matematica
per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 problemi.
Ok, se mi segui, sarà tutto più semplice! 😃
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 problemi.
Ok, se mi segui, sarà tutto più semplice! 😃
Problema n. 1
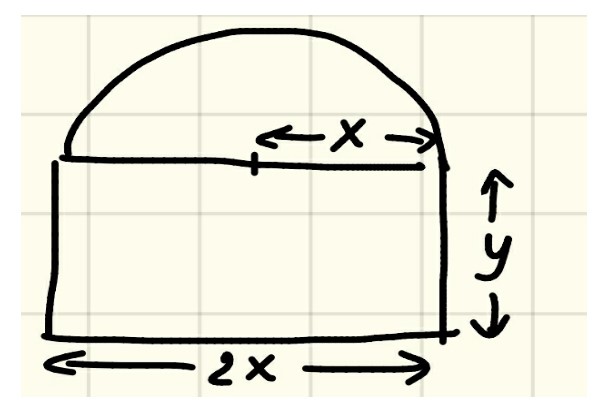
Caterina vuole progettare una finestra di forma rettangolare con un semicerchio sulla sommità. Se il perimetro totale deve essere 7,32 metri, quali dovrebbero essere le dimensioni affinché attraverso la finestra passi più luce possibile?
Trova la lunghezza del raggio del semicerchio e la misura dell'altezza del rettangolo. La forma della finestra è riportata qui sotto, nella fig. 2:
Svolgimento
Tra tutte le possibili finestre che hanno un perimetro totale uguale a 7,32 metri, dobbiamo trovare quella che ha la superficie massima, perché il problema ci dice che deve passare più luce possibile. Sappiamo che
7,32=2x+2y+π⋅x
Ti faccio notare che il secondo membro della precedente relazione rappresenta la lunghezza di tutto il bordo esterno della finestra, la cui forma geometrica è data dalla figura composta 'rettangolo+semicerchio' .
Andiamo avanti:
La superficie della finestra è data da:
Questa, evidenziata in verde, è la funzione di cui dobbiamo trovare il massimo.
Si tratta di una parabola con la concavità verso il basso, dato che il coefficiente di x² è negativo.
Visti gli scopi di questo tutorial, confermeremo l'informazione sulla concavità mediante il calcolo della derivata seconda.
Anche se, trattandosi di una parabola, possiamo seguire un' altra via, lo scopo di questa esercitazione è quello di sfruttare le derivate per
calcolare l'area massima
della finestra.
Importante, prima di passare alle derivate: quali sono i vincoli per le variabili x ed y?
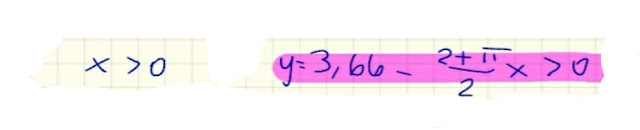 |
| Fig. 5 |
Entrambe devono essere positive perché esprimono rispettivamente la lunghezza del raggio del semicerchio e una dimensione del rettangolo.
Andando avanti, otteniamo esattamente l' intervallo all' interno del quale deve stare la x:
Adesso passiamo al calcolo delle derivate:
Come puoi vedere in fig. 7, abbiamo calcolato la derivata prima, f '(x), della funzione (area della finestra in funzione di x), l'abbiamo posta uguale a zero e abbiamo trovato la radice dell' equazione di primo grado
f '(x)=0
7,32-(4+π)x=0
Poi abbiamo scoperto, diciamo così, che la derivata seconda,
f ''(x), è negativa per ogni valore della x, confermando che la concavità è sempre rivolta verso il basso.
Dunque il punto stazionario che abbiamo trovato rappresenta un massimo della funzione:
Siccome questo valore della x, che annulla la derivata prima, rispetta il vincolo che abbiamo visto in precedenza, possiamo affermare che il raggio della porzione semicircolare della finestra "più luminosa", avente il perimetro uguale a 7,32 metri, è
x=7,32/(4+π)
L' altra dimensione (l'altezza della porzione rettangolare) è data da:
In conclusione, scopriamo che il raggio della porzione semicircolare e l'altezza della parte rettangolare sono uguali:
x=y=7,32/(4+π)
Prima di andare avanti col secondo problema, ci tengo a dirti che puoi imparare di più e finalmente puoi iniziare a migliorare i tuoi voti in matematica attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è
Matematica Quinquennio
Se vuoi imparare a risolvere gli esercizi di matematica con più serenità e abilità, allora è arrivato il momento di iniziare il tuo percorso gratuito; fai click sul link qui sotto:
Bene, torniamo al nostro secondo problemino!
Problema n. 2
Dobbiamo trovare il minimo della lunghezza del segmento AP, dove P è il punto generico del grafico della funzione.
P(x, x⁴/8)
Scriviamo dunque la lunghezza di questo segmento
AP in funzione di x:
Calcoliamo la sua derivata prima e ne studiamo il segno:
Osserviamo che questa derivata prima, per i valori della x dove essa ha senso, è positiva o nulla laddove il numeratore della frazione è maggiore o uguale a zero.
Perché?
Beh, perché nel dominio di questa derivata prima il denominatore della frazione che vediamo in fig. 13 sarà sempre positivo, dato che compare una radice quadrata, e il numeratore dovrà necessariamente essere positivo o nullo se vogliamo che il rapporto sia maggiore o uguale a zero.
Dunque poniamo il numeratore maggiore o uguale a zero e risolviamo la disequazione che si ottiene:
A questo punto, studiamo il segno dei due fattori presenti nel primo membro della disequazione:
La prima disequazione è banale!
La seconda disequazione viene risolta utilizzando una variabile ausiliaria,
t=x²
In questo modo, la seconda disequazione che dobbiamo studiare diventa
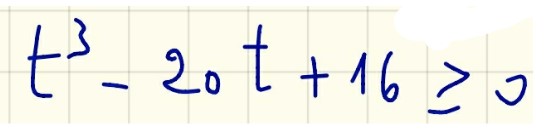
Adesso moltiplichiamo primo e secondo membro della disequazione per 8 e otteniamo:
Proviamo a scomporre questo polinomio di terzo grado, utilizzando la
regola di Ruffini
Notiamo che i coefficienti sono numeri interi, che il coefficiente dominante (cioè il numero che moltiplica t³) è 1 e che il termine noto è 16, quindi cerchiamo uno zero del polinomio tra i divisori di 16 :
±1, ±2, ±4, ±8, ±16
Se proviamo con 4, si ha:
4³-20⋅4+16=0
Ecco! Poiché 4 è uno zero del polinomio, possiamo passare alla
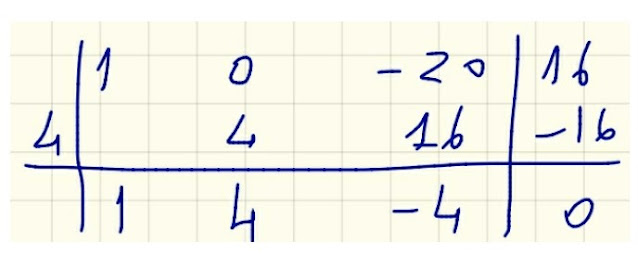
tabella di Ruffini
tenendo in considerazione il polinomio di terzo grado scritto così:
t³+0⋅t²-20⋅t+16
Adesso possiamo collocare correttamente i numeri in gioco nella tabella e fare i conti:
A questo punto, siamo in grado di riscrivere il nostro polinomio di terzo grado in questo modo:
La disequazione da risolvere viene riscritta così:
Ora è il momento di studiare i segni dei due fattori che vediamo in fig. 20:
 |
| Fig. 21 |
Pensiamo adesso alla seconda disequazione, cioè quella di secondo grado, e calcoliamo le radici della sua equazione associata:
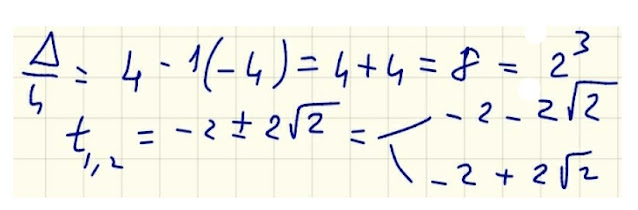 |
| Fig. 22 |
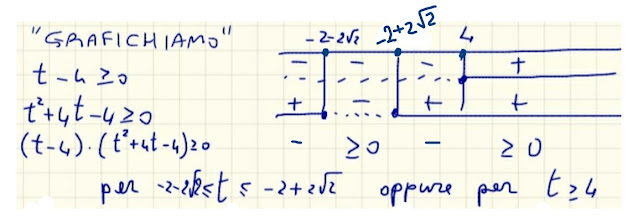
Adesso "grafichiamo" i segni dei due fattori:
 |
| Fig. 23 |
Come puoi vedere in fig. 23, il primo fattore,
t-4 ,
è maggiore di zero per i valori di t maggiori di 4, vale zero per t uguale a 4, ed è negativo per t minore di 4.
Il secondo fattore (fig. 23) è negativo nell' intervallo
]-2-2√2, -2+2√2[ ,
vale zero per
t=-2-2√2
e
t=-2+2√2 ,
ed è positivo altrove.
Pertanto, osservando i segni della fig. 20 possiamo stabilire dove il prodotto dei due fattori è positivo o nullo.
Le soluzioni della disequazione di fig. 20 sono i valori reali della variabile t che appartengono all' unione tra l' intervallo
[-2-2√2, -2+2√2]
e l'intervallo
[4, +∞[
Siccome avevo posto
t=x² , si ha che
t è positivo o nullo, e quindi possiamo restringere l'intervallo di appartenenza dei valori della variabile t :
A questo punto, ci troviamo tra le mani due disequazioni di secondo grado nell'incognita x, che andiamo subito a risolvere:
Ricordiamo da dove siamo partiti (fig. 14):
 |
| Fig. 26 |
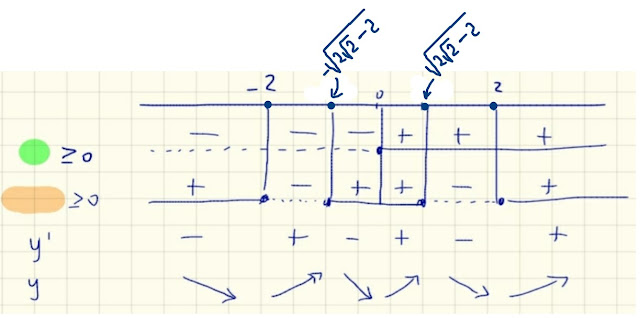
Adesso ricorriamo al nostro grafico dei segni dei due fattori (quello evidenziato in verde e quello evidenziato in arancione):
 |
| Fig. 27 |
Il segno del prodotto dei due fattori, che osserviamo nella fig. 27, coincide col segno della derivata prima, grazie al quale possiamo stabilire in quali intervalli la funzione "distanza", f(x), cresce o decresce.
Avevamo detto, vista la simmetria del problema, che avremmo preso in considerazione soltanto le
x≥0
Osserviamo che in x=0 e in x=2 abbiamo dei minimi relativi; vediamo quanto valgono queste distanze minime:
 |
| Fig. 28 |
Confrontando le due distanze, scopriamo che
f(2)<f(0)
Per concludere, possiamo scrivere che la distanza minima cercata è questa:
 |
| Fig. 29 |
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e scopri nel link qui sotto come puoi migliorare i tuoi voti in matematica:
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
Nel video qui sotto, puoi guardare lo svolgimento dei due problemi presentati in questo post. Buona visione!












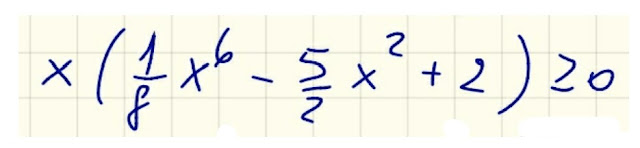
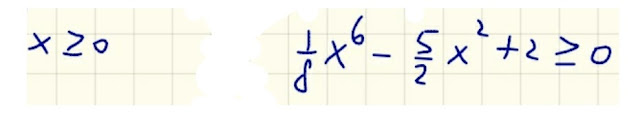


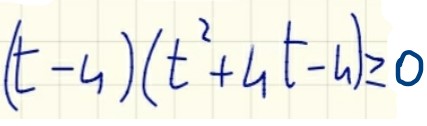












Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)