 |
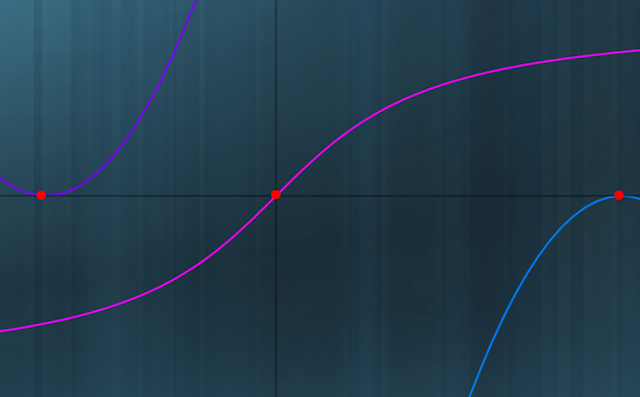
| Fig. 1 (Massimi, Minimi e Flessi delle Funzioni) |
Come si trovano i massimi, i minimi e i flessi di una funzione?
Ciao! Sono Giuseppe.
In questo blog pubblico
esercizi svolti di matematica
per le scuole superiori e l' università.
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi.
Ok, se mi segui, sarà tutto più semplice! 😃
Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.
In questo tutorial, ti propongo 2 esercizi.
Ok, se mi segui, sarà tutto più semplice! 😃
Trovare, se esistono, massimi/minimi relativi e flessi della funzione
Svolgimento
y = arctan(x)-x
Svolgimento
Si calcoli la derivata prima della funzione:
Ti ricordo che la derivata prima della funzione
y=arctan(x)
è
Studiamo la disequazione
y' ≥ 0
per vedere in quali intervalli cresce la funzione.
Questa disequazione è soddisfatta soltanto per
x=0
Per ogni (∀) valore di x≠0, si ha che la derivata prima della funzione è negativa:
Dunque la funzione, in questo caso particolare, è sempre decrescente.
In x=0 abbiamo una tangente orizzontale, perché per x=0 la derivata si annulla.
Adesso calcoliamo la derivata seconda della funzione:
Studiamo ora la disequazione
y'' > 0
Beh, la derivata seconda è positiva per valori negativi della x, è nulla per x=0, ed è negativa per valori positivi della variabile x.
Visualizziamo queste informazioni:
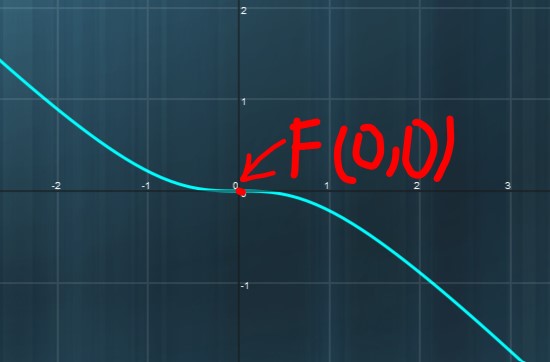
Ecco, la fig. 8 ci dice che in corrispondenza di x=0, in cui si annulla anche la derivata prima, assistiamo ad un cambio di concavità; per questo motivo possiamo affermare che la funzione assegnata possiede un flesso a tangente orizzontale di coordinate
(0, arctan(0)-0)
cioè
(0,0)
Prima di andare avanti col secondo esercizio, ci tengo a dirti che puoi imparare di più e finalmente puoi iniziare a migliorare i tuoi voti in matematica attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è
Matematica Quinquennio
Se vuoi imparare a risolvere gli esercizi di matematica con più serenità e abilità, allora è arrivato il momento di iniziare il tuo percorso gratuito; fai click sul link qui sotto:
Bene, torniamo agli esercizi!
L' esercizio n. 2 che svolgerò in questo tutorial chiede di...
Trovare, se ci sono, i punti di massimo/minimo relativo della funzione
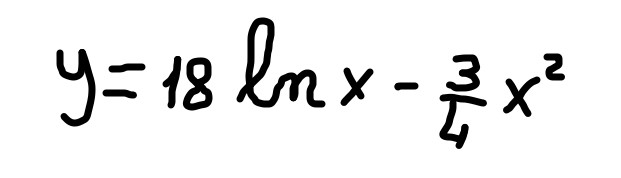 |
| Fig. 10 |
Svolgimento
Il dominio (D) di questa funzione è dato dall' insieme dei numeri reali positivi, che scriviamo così:
D={x∊R|x>0}
Calcoliamo la derivata prima:
Adesso studiamo la disequazione
y' ≥ 0
Andiamo avanti...
Adesso esaminiamo il segno del numeratore e quello del denominatore:
Risolviamo queste due semplici disequazioni.
Iniziamo da...
Numeratore maggiore di zero (N>0):
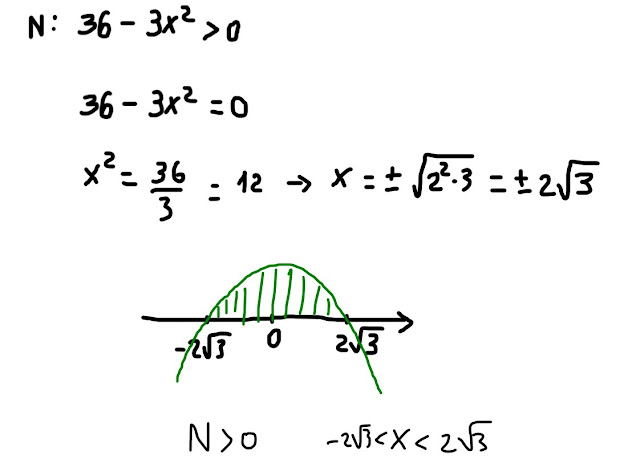 |
| Fig. 15 |
Come vedi nella fig. 15, l' equazione associata alla disequazione di secondo grado ci fornisce due radici:
-2√3, +2√3
Risolvendo per via grafica la disequazione, otteniamo che il numeratore è positivo per valori della x che appartengono all'intervallo
]-2√3, +2√3[
(estremi esclusi)
Non dimentichiamo che il dominio della funzione è dato da tutti i valori reali positivi (>0) della x.
Ora tocca a...
Denominatore maggiore di zero (D>0):
"Graficando" le informazioni sui segni del Numeratore e del Denominatore, abbiamo:
Il dominio della funzione sta tutto a destra dello zero (x>0).
Come si vede nella fig. 17, osservando soltanto la parte delle x positive, il numeratore è positivo per
x<2√3, è nullo per x=2√3, è negativo per x>2√3.
Il denominatore, invece, è positivo a destra dello zero.
Siamo così in grado di determinare il segno del rapporto tra numeratore (N) e denominatore (D), cioè il segno della derivata prima.
La fig. 17 ci mostra che la derivata prima (y') è positiva (funzione crescente) nell' intervallo in cui numeratore e denominatore hanno lo stesso segno; la derivata prima vale zero (tangente orizzontale) per x=2√3; per finire, la derivata prima è negativa (funzione decrescente) nell' intervallo in cui numeratore e denominatore hanno segni diversi.
Dunque la funzione assegnata presenta un punto di massimo relativo in x=2√3
Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e scopri nel link qui sotto come puoi migliorare i tuoi voti in matematica:
troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.
Alla prossima lezione. Ciao, ti aspetto!
Puoi seguire questa esercitazione nel video qui sotto👇:



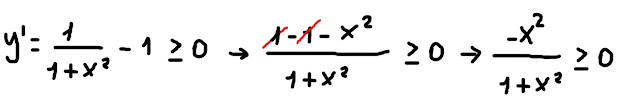





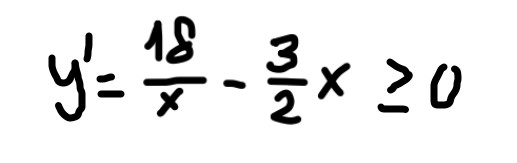














Nessun commento:
Posta un commento
Fammi sapere nei commenti i tuoi dubbi, le tue osservazioni, domande o semplicemente quello che pensi su ciò che hai letto.
Non si accettano commenti anonimi ;-)