Equazioni Goniometriche: Esercizi Svolti

Ultimo aggiornamento: 24/02/2021

Fig. 0

In questa esercitazione, ti faccio vedere

come si risolve un' equazione goniometrica.

Vediamo per quali valori di x è soddisfatta questa equazione particolare:

4sin(x)+1=0

Ciao! Sono Giuseppe.
In questo blog parlo di matematica, e in particolare svolgo e commento esercizi per le scuole superiori e l' università.

Se ti interessa la matematica, iscriviti al mio Canale Youtube e attiva la campanella per ricevere tutte le mie nuove pubblicazioni che arriveranno.

Svolgimento

4sin(x) + 1= 0 ⇒

⇒ 4sin(x) = -1 ⇒

⇒ sin(x) = -1/4

Domandiamoci: quali angoli (archi) hanno il seno (sin) che vale -1/4 ?

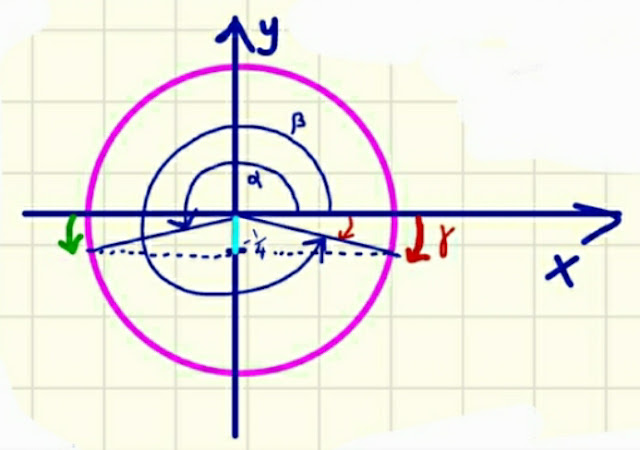
Rispondiamo a questo interrogativo disegnando una circonferenza goniometrica (circonferenza centrata nell' origine degli assi e di raggio uguale a 1) e individuiamo

-1/4 sull' asse y

Fig. 1

Prendiamo in esame la scrittura

arcsin(-1/4)

Cosa significa questa scrittura?

Significa:

l' arco il cui seno vale -1/4.

Prima di andare avanti, ci tengo a dirti che puoi imparare di più attraverso un' ampia raccolta di esercizi svolti e commentati da me in PDF stampabili. Sono centinaia e centinaia di esercizi per la scuola superiore! Il nome di questo mio ampio tutorial è

Matematica Quinquennio

Se vuoi scoprire di più e iniziare un percorso, fai click sul link qui sotto:

iscriviti gratis qui.

Bene, torniamo all' esercizio!

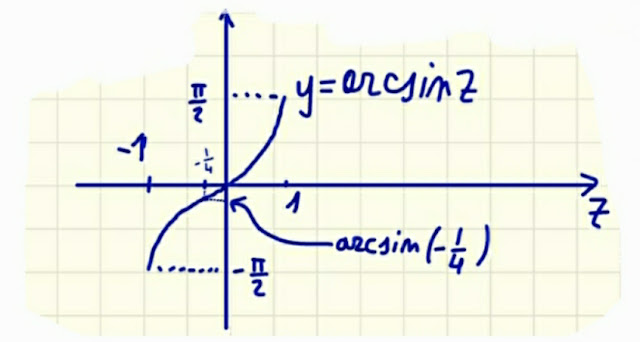
Dal grafico della funzione

y=arcsin(z)

che vedi qui sotto nella fig. 2, possiamo vedere quanto vale all' incirca proprio

arcsin(-1/4)

Ecco il grafico:

                     y

Fig. 2

La fig. 2 ci dice che

arcsin(-1/4) < 0

ed è rappresentato dall' archetto rosso orientato (verso orario) della fig. 1 

γ=arcsin(-1/4)

Dunque, guardando la fig. 3 qui sotto,

Fig. 3

possiamo dire che l' archetto verde orientato (verso antiorario) rappresenta un angolo uguale in ampiezza, ma di segno opposto, all' angolo rappresentato dall' archetto orientato rosso (verso orario).

Le possibili soluzioni dell' equazione di questo esercizio sono α (positivo, perché misurato nel verso antiorario: angolo piatto al quale si aggiunge l' angolino rappresentato dall' archetto orientato verde) oppure γ (negativo, perché misurato nel verso orario), con tutti i loro rispettivi omologhi.

Le soluzioni dell' equazione assegnata sono dunque:

x=π+[-arcsin(-1/4)]+2kπ

(primo gruppo di archi omologhi che soddisfano l' equazione data)

oppure

x=arcsin(-1/4)+2hπ

(secondo gruppo di archi omologhi che soddisfano l' equazione assegnata)

h, k rappresentano numeri interi relativi

☺️

Domanda: perché utilizzo due parametri, h e k, anziché uno solo?

Beh, perché il numero di giri che possiamo fare per raggiungere gli archi omologhi del primo gruppo NON deve essere necessariamente uguale al numero di giri che possiamo fare per raggiungere gli archi omologhi del secondo gruppo!

Se ti è piaciuto questo tutorial, fai clic su MI PIACE, condividi questo blog e dai un' occhiata ai link che trovi qui sotto: 

troverai "Matematica Quinquennio", un tutorial, in cui ho raccolto centinaia e centinaia di esercizi vari, in PDF scaricabili e stampabili, svolti e spiegati sugli argomenti più importanti che si studiano durante i cinque anni di scuola superiore.

Alla prossima lezione. Ciao, ti aspetto!