CREATIVITÀ NELLA MATEMATICA.

Segui @ilmatematto



" L' ispirazione, che consiste nell' ubbidire ciecamente ad ogni impulso, è in realtà una schiavitù. Il classico che scrive la sua tragedia osservando un certo numero di regole che conosce è più libero del poeta che scrive quel che gli passa per la testa ed è schiavo di altre regole che ignora. "

Raymond Queneau

Questa immagine non rappresenta nulla di particolare, è solo un esempio di espressione della libertà creativa.

Anche se può sembrare strano, la matematica, che molti considerano una scienza arida e rigida, ha 

ricevuto importanti impulsi da matematici creativi che non hanno avuto paura di sperimentare in totale libertà le idee che avevano in mente.

Un bell' esempio di creatività matematica, che mi piace condividere coi miei lettori, è quella del 

matematico Ulam, il quale, durante un convegno, forse per combattere la noia, si mise a "giocare" coi

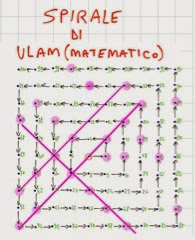
numeri naturali, disponendoli a spirale come nella figura sottostante che ho preparato(il numero 1 si trova al centro).

Poi cosa fece?

Evidenziò i numeri primi(che io ho messo in risalto col colore rosa) e si accorse che essi si disponevano lungo delle diagonali(alcune le ho tracciate), in particolare sembravano concentrarsi maggiormente su alcune diagonali.

(Per visualizzare l' immagine nitida, fai clic QUI)

Nell' immagine seguente(realizzata al computer durante un laboratorio di matematica computazionale), i puntini bianchi corrispondono ai numeri primi posti su una porzione della spirale di Ulam molto più grande di quella che sono riuscito a disegnare manualmente.

Si può notare, osservando una porzione maggiore di questa particolare spirale, che ci sono delle diagonali su cui la concentrazione dei numeri primi(puntini bianchi) sembra essere più alta rispetto ad altre diagonali.

Bene, la creatività di Ulam ha ampliato il dibattito all' interno della comunità matematica sulla distribuzione dei numeri primi.

Questo è uno dei tanti esempi che mi portano a essere a favore della libera ricerca, quella non condizionata da esigenze commerciali, militari o di altro tipo.

La libertà e la creatività nell' indagine scientifica possono portare, e la storia ce lo insegna, a risultati inaspettati più sorprendenti di quelli attesi.

Il mio augurio è che lo spirito del ricercatore possa svilupparsi tra gli studenti, partendo da una matematica sperimentale supportata dai computers e ovviamente da una forte curiosità stimolata da insegnanti motivati.