Funzioni: esercizi svolti di Matematica per la quinta superiore

In questa esercitazione di matematica, pensata per gli studenti del 5° anno di scuola superiore, vedremo lo svolgimento di almeno 8 esercizi dedicati alle funzioni: periodo di una funzione, funzione inversa, dominio e codominio etc.

Se vuoi ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.

Funzioni periodiche: che cosa sono?

Numeri Razionali: esercizi e problemi con le frazioni

In questa esercitazione, vedremo lo svolgimento di più di 8 esercizi di matematica per le Superiori, in particolare esercizi sulle frazioni, percentuali ed espressioni con potenze di numeri razionali.

Per non perderti i miei prossimi nuovi esercizi svolti, iscriviti gratis facendo click sull' immagine qui sotto:

Una volta iscritto, riceverai in omaggio, per email, la mia mini-guida su Come si studia la Matematica.

Se vuoi ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.

Ex. 1 di 8

Marco ha collezionato un quinto delle carte di una raccolta. Dopo averne trovate altre 10, possiede un terzo dell' intera raccolta. Quante carte compongono la collezione?

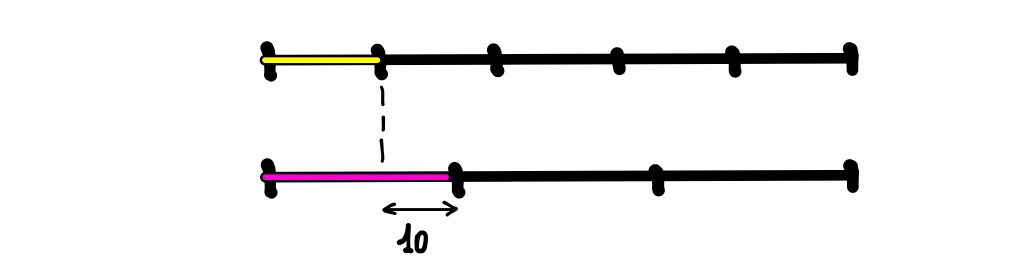
Rappresentiamo la totalità delle carte col segmento nero qui sotto, diviso in 5 parti uguali tra loro:



Marco ha collezionato 1/5 della raccolta (rappresentato dal segmentino giallo).


Dopo aver trovato altre 10 carte, Marco possiede 1/3 dell' intera raccolta:


Il segmento nero, che rappresenta la totalità delle carte, questa volta è suddiviso in 3 parti uguali.

Si può vedere, confrontando i segmenti, che quello di colore fucsia è più lungo di quello giallo; la loro differenza rappresenta le 10 carte in più:



1/3 - 1/5 = 2/15  corrisponde a 10 carte.

Ora, immaginiamo di dividere il segmento che rappresenta l' intera raccolta di carte in 15 parti: 2 parti corrispondono a 10 carte.

Sfruttiamo adesso una proporzione...

Se hai dubbi, osservazioni, non esitare a lasciare  un commento qui sotto ✍✍✍

Indichiamo con la lettera x il numero incognito di tutte le carte e scriviamo

2 : 10 = 15 : x  ( si legge così: 2 parti stanno a 10 carte come 15 parti stanno a x carte)

La proporzione che abbiamo scritto significa che 2 parti rappresentano 10 carte come 15 parti rappresentano tutte le x carte.

Da cui si ottiene che  x = (10×15):2 = 75

Ecco, le carte, in tutto, sono 75.

Ex. 2 di 8

Due amici, che abitano nella stessa strada ma da parti opposte, si danno appuntamento ed escono di casa per incontrarsi. Dopo un certo tempo, uno dei due ha percorso i 2/5 della strada, l' altro ha percorso i 3/7, e la loro distanza è pari a 600 metri. Trovare quanto è lunga la strada.

Utilizziamo i segmenti colorati per avere le idee più chiare.

Hai bisogno di una buona Calcolatrice Scientifica?
Scopri qual è quella più diffusa tra i miei studenti, in questo momento. 😊



Come si può vedere nella figura, i due segmenti bianchi (quello superiore è suddiviso in 5 parti uguali, quello inferiore invece è suddiviso in 7 parti uguali) rappresentano la stessa strada che i due amici percorrono per incontrarsi.

Uno esce di casa, posta nel punto A, e cammina verso destra percorrendo i 2/5 della strada (tratto giallo); l' altro esce di casa, posta nel punto B, e cammina verso sinistra percorrendo i 3/7 della strada (tratto fucsia).

Mettendo a confronto il segmento bianco frazionato superiore con quello bianco frazionato inferiore, possiamo vedere che la differenza tra lunghezza del tratto blu e la lunghezza del tratto giallo ci fornisce proprio la distanza tra i due amici richiesta dal nostro problema.

Il tratto blu corrisponde a 4/7.

Adesso calcoliamo la differenza 4/7 - 2/5 .

Quanto fa?



Fa 6/35, che rappresenta la distanza (600 metri) tra i due amici in quel momento.

Quindi, praticamente, possiamo pensare di suddividere tutta la strada in 35 parti uguali e 6 parti corrispondono a 600 metri.

Una parte è dunque lunga 100 metri.

Pertanto basta moltiplicare 100 metri per 35 (l' intera strada è suddivisa in 35 parti) e otteniamo 3500 metri.

Le case dei due amici sono distanti 3,5 km l' una dall' altra.

Ex. 3 di 8

Acquistiamo un maglione a 70€. E' stato applicato uno sconto del 30%. Qual era il prezzo di partenza e a quanto ammonta lo sconto?

Andiamo a risolvere pure questo problemino.

Stai cercando una buona e poco costosa calcolatrice grafica senza calcolo simbolico?
Guarda questa.

Sfruttiamo anche questa volta i segmenti.



Questo segmento giallo rappresenti il prezzo intero del maglione (il prezzo prima dello sconto).

Dividiamo l' intero prezzo (segmento giallo) in 100 parti uguali e...



togliamo 30 parti (lo sconto del 30%).

70 parti su 100 corrispondono a 70€, quindi 1 parte su 100 vale 1€.

Pertanto concludiamo dicendo che il prezzo intero (100 parti) è 100€ e lo sconto applicato ammonta a 30€.

Dai un' occhiata alle mie raccolte di esercizi che ho ampiamente svolto e commentato:

Ex. 4 di 8

Calcoliamo la seguente "cascata di frazioni":

Vediamo insieme i passaggi.

Per non perderti i miei prossimi nuovi esercizi svolti, iscriviti gratis facendo click sull' immagine qui sotto:


Una volta iscritto, riceverai in omaggio la mia mini-guida su Come si studia la Matematica.

Se vuoi ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.

= 1 + 3/5 = 8/5

Su Amazon puoi trovare veramente di tutto. Fai click qui sotto:

Ex. 5 di 8

Guarda questo video sui numeri razionali, in cui sono svolti esercizi di base per ripassare velocemente i numeri razionali, le percentuali, le proporzioni, le espressioni con potenze.

Se stai cercando anche libri scolastici, puoi trovarli su Amazon. Fai click qui sotto:

Ex. 6 di 8

Guarda questo video sui numeri razionali, in cui svolgo un' espressione contenente potenze di numeri razionali.

Qui trovi tantissime altre idee per il tuo Shopping.

Ex. 7 di 8

Guarda anche questo video sui numeri razionali, in cui svolgo un' altra espressione contenente potenze.

Ora, prima di lasciarti il link ad un ulteriore video ( ex. 8 ) in cui mostro come trasformare alcune frazioni in percentuali, leggi gli ultimi tre inviti che ho per te:

1) Se sei una persona che ama imparare nuove lingue o, in generale, nuove competenze o abilità, allora ti consiglio di guardare questo link per scegliere fra tantissimi corsi online di formazione presenti sulla piattaforma.

2) Seguimi sui tuoi Social preferiti; ci vediamo anche lì, ti aspetto! 😊

3) Aiutaci, con una donazione, a realizzare altre esercitazioni gratuite come questa.
Inoltre, puoi condividere questa lezione, e ti invito a iscriverti, se non lo hai ancora fatto.

Ex. 8 di 8

Guarda questo video sulle percentuali.

Ciao, a presto!

Equazioni e Disequazioni con Valore Assoluto: esercizi svolti

ultimo aggiornamento: 01 12 2020

In questa esercitazione, vedremo lo svolgimento, nei dettagli, di 3 esercizi di matematica per le Superiori; in particolare affronteremo 2 equazioni e 1 disequazione con valore assoluto.

Imparerai a risolvere, col giusto metodo, equazioni e disequazioni in cui sono presenti queste "cose strane" che si chiamano valori assoluti, o moduli, e che fanno sembrare orribili le dis-equazioni. 😲

Tranquilli, se mi seguite, sarà tutto più semplice! 😃

Se vuoi questa lezione in PDF stampabile, sempre a portata di mano, consultabile tutte le volte che vuoi, allora fai click sul pulsante qui sotto e scopri come ottenerla:

👇

Ottieni il PDF Stampabile

👆

Esercizio 1 di 3

Come si risolve un' equazione col valore assoluto

Risolvere questa equazione:

2•|3+x| + 3x = |x-1| - 4x

Ricordiamo la definizione di valore

assoluto e poi facciamo un esempio:

Fig. 1.1

Questa scrittura che vedi nella

figura 1.1 significa che il valore

assoluto di a (argomento) è uguale

ad a, se a è maggiore o uguale a

zero,

oppure

il valore assoluto di a (argomento) è uguale a  - a, se a è minore di zero.


Proviamo a fare un primo esempio

attribuendo ad a il valore -7.
Calcoliamo, seguendo la definizione

di fig. 1.1, il valore assoluto di -7:

| -7 | = -( -7) = 7, perchè -7 < 0

E quanto vale | 7 | ?
L' argomento, questa volta, è 7 ( ≥ 0 ), quindi | 7 | = 7

Esempio:

Fig. 1.2

Nella fig. 1.2 non abbiamo fatto altro

che applicare la definizione di

valore assoluto (modulo), che vedi

nella figura 1.1, per "sciogliere",

diciamo così, il valore assoluto di

x - 1 .

In pratica, possiamo “sciogliere”

il valore assoluto di x - 1,

scrivendo che

|x - 1|=x - 1, se x - 1 ≥ 0,

cioè se x ≥ 1

oppure

|x - 1|= - (x - 1) = -x + 1,

se x - 1 < 0,

cioè se x < 1

Non spaventatevi, perchè faremo

degli esercizi più sostanziosi,

e così capiremo meglio.

Studiamo il segno di ogni

espressione “ingabbiata” nel

valore assoluto (  | … |  )

Prima di andare avanti, ti invito a non perderti i miei prossimi nuovi esercizi svolti: iscriviti gratis.

Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.

Se vuoi invece ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.

Torniamo al nostro 1° esercizio.

Ci conviene studiare il segno di ogni

espressione “ingabbiata” nel

valore assoluto (  | … |  ).

Riprendiamo la nostra equazione:

2•|3+x| + 3x = |x-1| - 4x

Le espressioni ingabbiate nel valore

assoluto sono 3+x e x-1, di cui

studieremo il segno.

3+x > 0 ⟶ x > -3
x-1 > 0 ⟶ x > 1

Facciamo il grafico con le linee dei

segni:

Fig 1.3

L' argomento del primo valore

assoluto, 3+x, è positivo per

x > -3, è negativo per x < -3

e nullo per x = -3.
L' argomento del secondo

valore assoluto, x-1, è

positivo per x > 1, è negativo
per x < 1 e nullo per x = 1.

Stando alla definizione di figura 1.1,

possiamo "sciogliere" i valori

assoluti della nostra equazione

assegnata in questo modo:

eq.1:

2•[-(3+x)] + 3x = -(x-1) - 4x

ed x < -3

oppure

eq.2:

2•(3+x) + 3x = -(x-1) - 4x

e -3 ≤ x < 1

oppure

eq.3:

2•(3+x) + 3x = x-1 - 4x

ed x ≥ 1

Risolviamo queste tre equazioni,

tenendo conto delle loro rispettive

restrizioni sulla x.

Se hai dubbi, osservazioni, non esitare a lasciare  un commento qui sotto ✍✍✍







Perché c' è la faccetta triste?
Perché 7/6 non è minore di -3

(7/6 non è accettabile!)



Qui la faccina è allegra perchè -1/2 è compreso tra -3 e 1, quindi x = -1/2 è accettabile.





Anche -7/8 non si può accettare. Perchè?

Per concludere il discorso sull' equazione del 1° esercizio, la sua soluzione è x = -1/2.

Avanti con l'

Esercizio 2 di 3

Come si risolve un' equazione col valore assoluto

Se hai un' azienda o conosci qualcuno che la possiede, potrebbe esserti molto utile Amazon Business. L' iscrizione è gratuita! ⚙🔝

Risolviamo questa seconda equazione:

Beh, diciamo subito che x ≠ 1, perché

altrimenti si azzera il denominatore,

|1-x|.

Studiamo il segno di ogni

espressione “ingabbiata” nel

valore assoluto.

x > 0
2 + x > 0 ⟶ x > -2
1 - x > 0 ⟶ x < 1

Facciamo il grafico con le linee dei

segni:

Hai bisogno di una buona Calcolatrice Scientifica?
Scopri qual è quella più diffusa tra i miei studenti, in questo momento. 😊

Stando alla definizione di figura 1.1,

possiamo "sciogliere" i valori assoluti

della nostra equazione assegnata in

questo modo:

oppure

oppure

oppure

Risolviamo queste quattro equazioni,

tenendo conto delle loro rispettive

restrizioni sulla x.






Andiamo avanti:



La faccina è triste perchè 4/3 NON è minore di -2. La condizione, qui, è x < -2

4/3 NON è accettabile! 

Ancora avanti:








Perché 0 e 1/2, qui, sono entrambi inaccettabili?

Perché non soddisfano la condizione -2 ≤ x < 0


Prima di andare avanti con la terza equazione e le sue restrizioni sulla x, ti chiedo se stai cercando una buona e poco costosa calcolatrice grafica senza calcolo simbolico.
Guarda questa.







Come vedi, adesso siamo autorizzati ad accettare x=0 come soluzione, perchè soddisfa la condizione
0 ≤ x < 1

Procediamo verso la quarta equazione.

Dai anche un' occhiata alle mie raccolte di esercizi che ho ampiamente svolto e commentato.

In questo momento sono pure disponibili questi miei 3 ebooks:
- Monomi (20 esercizi svolti e commentati);
- Grafici con le Trasformazioni Geometriche (13 esercizi svolti e commentati);
- Principio di Induzione ( 7 esercizi svolti e commentati ).








Anche 2 è accettabile perché

2 > 1

Concludiamo dicendo che l' equazione coi valori assoluti del nostro secondo esercizio ha le seguenti soluzioni:

x = 0 , x = 2

Tra un po' affronteremo una disequazione coi valori assoluti.


Per non perderti i miei prossimi nuovi esercizi svolti, iscriviti gratis.

Una volta iscritto, riceverai, per email, anche i miei 7 Consigli su Come si studia la Matematica.

Se vuoi ricevere gli aggiornamenti sulla pubblicazione dei miei nuovi video di matematica, iscriviti al mio Canale Youtube.

Esercizio 3 di 3

Come si risolve una disequazione col valore assoluto

Risolviamo questa disequazione:

| 2(x - 1) | < | x - 16 | + 2x

Studiamo il segno di ogni

espressione che troviamo nel

valore assoluto.

Poniamo queste espressioni > 0:

2(x - 1) > 0

x - 16 > 0

Sono due semplici disequazioni di 1° grado, che risolviamo:

2(x - 1) > 0  ⟶  x > 1

x - 16 > 0  ⟶  x > 16

Visualizziamo queste informazioni

disegnando le linee dei segni.

Fai un salto su Amazon, dove puoi trovare veramente di tutto. Fai click qui sotto:

Sapendo dove gli argomenti dei valori assoluti sono positivi o nulli e dove invece sono negativi, ricordando la definizione vista in fig. 1.1, andiamo a "sciogliere" la nostra disequazione assegnata.

Per x < 1, entrambi gli argomenti sono negativi, quindi riscriviamo la disequazione assegnata così:

-2(x - 1)  <  -( x - 16 ) + 2x

Per 1 ≤ x < 16, il 1° argomento è positivo o nullo e il 2° argomento è negativo, quindi riscriviamo la disequazione assegnata così:

2(x - 1)  <  - (x - 16) + 2x

Per x ≥ 16, entrambi gli argomenti sono positivi o nulli, quindi riscriviamo la disequazione assegnata così:

2(x - 1) <  x - 16 + 2x    

Dunque dobbiamo risolvere, in pratica, questi tre sistemi, e poi faremo l' unione tra le soluzioni che avremo trovato:

Cominciamo a risolvere il 1° sistema.

Se stai cercando anche libri scolastici, puoi trovarli su Amazon. Fai click qui sotto:

Se hai dubbi, osservazioni, o qualche richiesta di chiarimenti, fammi sapere nei commenti; proverò a risponderti compatibilmente con tutti gli altri miei impegni. 😉

E ora visualizziamo con un disegno queste ultime informazioni che si riferiscono alla x, per vedere se ci sono intervalli in cui sono soddisfatte entrambe le disequazioni di questo 1° sistema.

Ripassa un po' come si risolvono i sistemi di disequazioni (puoi andare direttamente al paragrafo 6, che si trova in fondo all' esercitazione).

Come puoi vedere, le due disequazioni del sistema in esame sono soddisfatte nell' intervallo

-14/3 < x < 1  (estremi esclusi)

Risolviamo il 2° sistema.

Qui trovi tantissime altre idee per il tuo Shopping.

Visualizziamo, come al solito, queste ultime informazioni relative alla x:



Domanda: in quale intervallo è risolto questo 2° sistema?
Risposta: 1 ≤ x < 16

Risolviamo il 3° sistema:

Disegniamo le nostre utilissime linee continue/discontinue per vedere bene queste ultime informazioni relative alla x:



Bene, il nostro 3° sistema è risolto nell' intervallo

x ≥ 16

Non è ancora finita!
Dobbiamo fare l' unione ( ⋃ ) tra le tre "soluzioni":

-14/3 < x < 1  ⋃  1 ≤ x < 16  ⋃ 

⋃  x ≥ 16

Rappresentiamo con un disegno colorato questi tre intervalli, che poi uniremo.
Sarà interessante "vedere" l' intervallo risultante.

Seguimi sui tuoi Social preferiti; ci vediamo anche lì, ti aspetto! 😊

Se ora li uniamo, otteniamo:




Questo è l' intervallo risultante e rappresenta le soluzioni della disequazione del nostro terzo e ultimo esercizio di questa esercitazione.

Come possiamo scrivere queste soluzioni con un linguaggio più formale?
Vediamolo!

Aiutaci, con una donazione, a realizzare altre esercitazioni gratuite come questa, che, come puoi immaginare, richiede molto impegno e attenzione.
Inoltre, puoi condividere questa lezione, e ti invito a iscriverti, se non lo hai ancora fatto.

Le soluzioni sono:

S = { x ∈ R |  x > -14/3 }

Ciao, a presto!

Puoi guardare questa esercitazione nel video qui sotto: